Question

2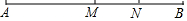．如图所示，点M，N是线段AB上的两个点，且M是AB的中点，N是MB的中点，若AB=a，NB=b，下列结论：①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a．其中正确的有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 根据线段的中点定义可得AM=MB=$\frac{1}{2}$AB，BN=NM=$\frac{1}{2}$BM，再根据线段之间的和差关系列出等式即可．

解答 解：解：∵M是线段AB的中点，
∴AM=MB=$\frac{1}{2}$AB=$\frac{1}{2}$a，故①正确；
AN=AB-BN=a-b，故②正确；
MN=MB-NB=$\frac{1}{2}$AB-BN=$\frac{1}{2}$a-b，故③正确；
∵M是线段AB的中点，N是AM的中点，
∴AM=BM=$\frac{1}{2}$AB=$\frac{1}{2}$a，MN=$\frac{1}{2}$MB=$\frac{1}{2}$×$\frac{1}{2}$a=$\frac{1}{4}$a，故④正确；
故选：D．

点评 此题主要考查了线段的中点，关键是掌握线段的中点把线段分成相等的两部分．