题目内容
 如图,AD∥BC,∠D=90°,DC=5,AD=2,BC=3,点P在线段DC上,问:当PC的长为何值时,△PAD与△PBC相似?
如图,AD∥BC,∠D=90°,DC=5,AD=2,BC=3,点P在线段DC上,问:当PC的长为何值时,△PAD与△PBC相似?考点:相似三角形的判定
专题:
分析:根据已知分两种情况△PAD∽△PBC或△PAD∽△CBP来进行分析,求得PD的长,从而确定PC的长.
解答:
 解:∵AD∥BC,∠D=90°
解:∵AD∥BC,∠D=90°
∴∠C=∠D=90°
∵DC=5,AD=2,BC=3.
设PD=x,则PC=5-x;
①若PD:PC=AD:BC,则△PAD∽△PBC
∴
=
,
解得:x=2,
PC=5-x=3;
②若PD:BC=AD:PC,则△PAD∽△CBP
∴
=
,
解得:x=2或x=3,
PC=5-x=3或2.
故当PC的长为2或3时,△PAD与△PBC相似.

 解:∵AD∥BC,∠D=90°
解:∵AD∥BC,∠D=90°∴∠C=∠D=90°
∵DC=5,AD=2,BC=3.
设PD=x,则PC=5-x;
①若PD:PC=AD:BC,则△PAD∽△PBC
∴
| x |
| 5-x |
| 2 |
| 3 |
解得:x=2,
PC=5-x=3;
②若PD:BC=AD:PC,则△PAD∽△CBP
∴
| x |
| 3 |
| 2 |
| 5-x |
解得:x=2或x=3,
PC=5-x=3或2.
故当PC的长为2或3时,△PAD与△PBC相似.
点评:此题考查了相似三角形的判定:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列各数不能与1,3,
成比例的是( )
| 2 |
A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,某拦河坝的横断面为梯形ABCD,若坝顶AD=3m,坝底BC=
如图,某拦河坝的横断面为梯形ABCD,若坝顶AD=3m,坝底BC= 如图,在⊙O中,直径AB⊥弦CD于点E.若BE=
如图,在⊙O中,直径AB⊥弦CD于点E.若BE=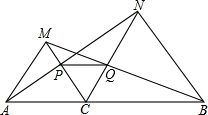 如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由. 如图,在平面直角坐标系中有△ABC.
如图,在平面直角坐标系中有△ABC.