题目内容
7.计算:(1)(-$\frac{1}{3}$)÷(-$\frac{1}{3}$)2-4×(-$\frac{1}{2}$)3
(2)-12016×[4-(-3)2]+3÷(-$\frac{3}{4}$)
分析 (1)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-$\frac{1}{3}$×9+4×$\frac{1}{8}$=-3+$\frac{1}{2}$=-2$\frac{1}{2}$;
(2)原式=-1×(-5)-4=5-4=1.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
18.已知正比例函数y=3x的图象经过点(-1,m),则m的值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
15.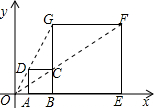 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )| A. | (2,2) | B. | (3,1) | C. | (3,2) | D. | (4,2) |
19.下列分式约分,正确的是( )
| A. | $\frac{{a}^{6}}{{a}^{3}}$=a2 | B. | $\frac{2a{b}^{2}}{6{a}^{2}{b}^{2}}$=$\frac{1}{3}$ | C. | $\frac{m+n}{{m}^{2}+mn}$=$\frac{1}{m}$ | D. | $\frac{x-y}{x-y}$=0 |
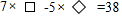 老师在课下给同学们留了如图所示的一个等式,让同学自己出题,并作出答案,请你回答处下列两个同学所提出问题的答案.
老师在课下给同学们留了如图所示的一个等式,让同学自己出题,并作出答案,请你回答处下列两个同学所提出问题的答案.