题目内容
15.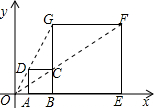 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A、B、E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )| A. | (2,2) | B. | (3,1) | C. | (3,2) | D. | (4,2) |
分析 根据位似图形的概念和性质列出比例式,求出OB、CD,求出点C的坐标.
解答 解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,
∴$\frac{OB}{OE}$=$\frac{1}{3}$,$\frac{CD}{GF}$=$\frac{OD}{OG}$=$\frac{1}{3}$,
即$\frac{OB}{OB+6}$=$\frac{1}{3}$,$\frac{CD}{6}$=$\frac{1}{3}$,
解得,OB=3,CD=2,
∴点C的坐标为(3,2),
故选:C.
点评 本题考查的是位似变换的性质、正方形的性质,掌握位似图形的两个图形是相似形是解题的关键.

练习册系列答案
相关题目
3.下面计算正确的是( )
| A. | 3x+2y=6xy | B. | x+x=x2 | C. | 9a2b-9a2b=0 | D. | -9y2+6y2=-3 |
20.若(a+3)2+|b-2|=0,则ab的值是( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
7.计算:
(1)(-$\frac{1}{3}$)÷(-$\frac{1}{3}$)2-4×(-$\frac{1}{2}$)3
(2)-12016×[4-(-3)2]+3÷(-$\frac{3}{4}$)
(1)(-$\frac{1}{3}$)÷(-$\frac{1}{3}$)2-4×(-$\frac{1}{2}$)3
(2)-12016×[4-(-3)2]+3÷(-$\frac{3}{4}$)
5. 如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )
如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )
 如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )
如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )| A. | 80×10-9米 | B. | 8.0×10-8米 | C. | 8.0×10-9米 | D. | 0.8×10-9米 |
 如图,四边形ABCD中,AB=BC=1,CD=$\sqrt{3}$,DA=1,且∠B=90°.
如图,四边形ABCD中,AB=BC=1,CD=$\sqrt{3}$,DA=1,且∠B=90°.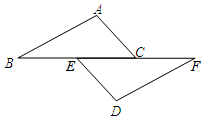 如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF,
如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF,