题目内容
16.若多项式mx3-2x2+3x-2x3+5x2-nx+1不含三次项及一次项,请你确定m,n的值,并求出mn+(m-n)2016的值.分析 先将关于x的多项式合并同类项.由于其不含三次项及一次项,即系数为0,可以先求得m,n,再求出mn+(m-n)2016的值.
解答 解:mx3-2x2+3x-2x3+5x2-nx+1=(m-2)x3+3x2+(3-n)x+1,
因为不含三次项及一次项的多项式,依题意有
(1)m-2=0,m=2;(2)3-n=0,n=3.
代入mn+(m-n)2016,原式=23+(-1)2016=9.
点评 此题考查了多项式的定义,解答本题必须先合并同类项,否则容易误解为m=0,n=0.

练习册系列答案
相关题目
7.计算:
(1)(-$\frac{1}{3}$)÷(-$\frac{1}{3}$)2-4×(-$\frac{1}{2}$)3
(2)-12016×[4-(-3)2]+3÷(-$\frac{3}{4}$)
(1)(-$\frac{1}{3}$)÷(-$\frac{1}{3}$)2-4×(-$\frac{1}{2}$)3
(2)-12016×[4-(-3)2]+3÷(-$\frac{3}{4}$)
11.下列各单项式中,与2xy是同类项的是( )
| A. | xy | B. | 3y | C. | 2x3y2 | D. | 4x |
5. 如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )
如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )
 如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )
如图,去年埃博拉病毒在部分国家蔓延,夺走了很多人的生命,埃博拉病毒直径约为80纳米(1纳米=0.000000001米),用科学记数法表示这个病毒直径的大小,正确的是( )| A. | 80×10-9米 | B. | 8.0×10-8米 | C. | 8.0×10-9米 | D. | 0.8×10-9米 |
 如图,四边形ABCD中,AB=BC=1,CD=$\sqrt{3}$,DA=1,且∠B=90°.
如图,四边形ABCD中,AB=BC=1,CD=$\sqrt{3}$,DA=1,且∠B=90°.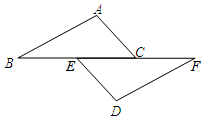 如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF,
如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF, 如图,点P是以AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是-$\sqrt{10}$+1.
如图,点P是以AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是-$\sqrt{10}$+1. 一个几何体是由一些大小相同的小正方体摆成的,其主视图和左视图如图,则组成的这个几何体的小正方体最多有10块.
一个几何体是由一些大小相同的小正方体摆成的,其主视图和左视图如图,则组成的这个几何体的小正方体最多有10块.