题目内容
16.对于整数a、b、c、d符号$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$表示运算ad-bc,已知1<$|\begin{array}{l}{1}&{b}\\{4}&{d}\end{array}|$<3,-2<$|\begin{array}{l}{-1}&{b}\\{-2}&{d}\end{array}|$<1,则b+d的值是-3或2.分析 根据行列式$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$表示运算ad-bc,可得不等式组,根据不等式的性质,可得-1<-2b<4,再根据不等式的性质3,可得b的范围,根据整数的定义,可得b的值,根据不等式的性质,可得d的值,根据有理数的加法,可得答案.
解答 解:由1<$|\begin{array}{l}{1}&{b}\\{4}&{d}\end{array}|$<3,-2<$|\begin{array}{l}{-1}&{b}\\{-2}&{d}\end{array}|$<1,得$\left\{\begin{array}{l}{1<b-4d<3①}\\{-2<-d+2b<1②}\end{array}\right.$,
①+②,得-1<-2b<4,
解得-2<b<$\frac{1}{2}$,
∵a、b、c、d都是整数,
∴b=-1或b=0,
当b=-1时,1<d+4<3,解得-3<d<-1,∴d=-2,b+d=-1+(-2)=-3;
当b=0时,1<d<3,∴d=2,b+d=2+2=2,
故答案为:-3或2.
点评 本题考查了不等式的性质,利用$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$表示运算ad-bc得出不等式组是解题关键,又利用了不等式的性质:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
8. 已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )
已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )
 已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )
已知:如图,∠A=25°,∠CED=95°,∠D=40°,则∠B的度数为( )| A. | 20° | B. | 160° | C. | 120° | D. | 65° |

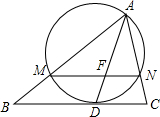 如图,在△ABC中,已知AB=9,BC=8,CA=7,AD为内角平分线,以AD为弦作一圆.该圆与BC相切,与AB交于M,与AC交于N,则BM+CN=4.
如图,在△ABC中,已知AB=9,BC=8,CA=7,AD为内角平分线,以AD为弦作一圆.该圆与BC相切,与AB交于M,与AC交于N,则BM+CN=4.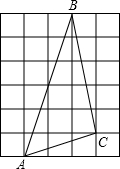 如图,图中的小方格都是边长为1的正方形,若A(-x,$\frac{-3y+6}{2}$),B(2x-1,$\frac{2y+1}{3}$),C(z+1,$\frac{2z-8}{3}$),已知A、B关于原点对称,C在二、四象限平分线上.
如图,图中的小方格都是边长为1的正方形,若A(-x,$\frac{-3y+6}{2}$),B(2x-1,$\frac{2y+1}{3}$),C(z+1,$\frac{2z-8}{3}$),已知A、B关于原点对称,C在二、四象限平分线上.