题目内容
7.(1)试说明无论x为何值,代数式(x-1)(x2+x+1)-(x2+1)(x+1)+x(x+1)的值等于一个常数.(2)试比较3555,4444,5333的大小.
分析 (1)原式利用立方公式和因式分解变形为x3-1-(x+1)(x2-x+1),再利用立方公式变形为x3-1-(x3+1),再去括号合并得到结果为常数,即可得到结果与x值无关.
(2)先变为指数相同,再比较底数的大小即可求解.
解答 解:(1)(x-1)(x2+x+1)-(x2+1)(x+1)+x(x+1)
=x3-1-(x+1)(x2-x+1)
=x3-1-(x3+1)
=x3-1-x3-1
=-2,
∵结果为常数,
∴无论x为何值,代数式(x-1)(x2+x+1)-(x2+1)(x+1)+x(x+1)的值等于一个常数.
(2)∵3555=243111,4444=256111,5333=125111,
256>243>125,
∴4444>3555>5333.
点评 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.建立平面直角坐标系选择一个适当的参照点为( ),确定x轴、y轴的正方向.
| A. | 坐标 | B. | 原点 | C. | 单位长度 | D. | 图形 |
15.计算下列各题:
(1)-20+(-14)-(-18)-13
(2)(-3)×(-18)÷(-6)÷3
(3)$\frac{7}{4}$÷$\frac{7}{8}$-$\frac{2}{3}$×(-6)
(1)-20+(-14)-(-18)-13
(2)(-3)×(-18)÷(-6)÷3
(3)$\frac{7}{4}$÷$\frac{7}{8}$-$\frac{2}{3}$×(-6)
2.下列说法正确的是( )
| A. | 面积相等的两个三角形全等 | B. | 周长相等的两个三角形全等 | ||
| C. | 形状相同的两个三角形全等 | D. | 成轴对称的两个三角形全等 |
19.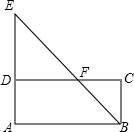 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{BC}$=$\frac{EF}{FB}$ | B. | $\frac{DE}{AD}$=$\frac{DF}{AB}$ | C. | $\frac{BC}{DE}$=$\frac{CF}{DF}$ | D. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ |



