题目内容
8．
已知：如图，∠A=25°，∠CED=95°，∠D=40°，则∠B的度数为（ ）| A． | 20° | B． | 160° | C． | 120° | D． | 65° |
分析 先根据三角形外角性质求出∠BFD=65°，再利用对顶角相等得到∠BEF=∠CED=95°，然后在△BEF中利用三角形内角和可计算出∠B的度数．
解答 解：∵∠BFD=∠A+∠D，
∴∠BFD=25°+40°=65°，
而∠BEF=∠CED=95°，
∴∠B=180°-∠BEF-∠BFE=180°-95°-65°=20°．
故选A．
点评 本题考查了三角形内角和定理：三角形内角和是180°．三角形内角和主要用在求三角形中角的度数．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
19．
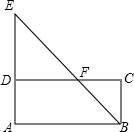如图，点F是矩形ABCD的边CD上一点，射线BF交AD的延长线于点E，则下列结论错误的是（ ）
如图，点F是矩形ABCD的边CD上一点，射线BF交AD的延长线于点E，则下列结论错误的是（ ）| A． | $\frac{ED}{BC}$=$\frac{EF}{FB}$ | B． | $\frac{DE}{AD}$=$\frac{DF}{AB}$ | C． | $\frac{BC}{DE}$=$\frac{CF}{DF}$ | D． | $\frac{BF}{BE}$=$\frac{BC}{AE}$ |
18．方程3x2-2=1-4x的两个根的和为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{1}{3}$ | C． | -$\frac{2}{3}$ | D． | -$\frac{4}{3}$ |