题目内容
11.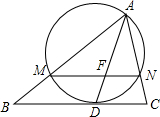 如图,在△ABC中,已知AB=9,BC=8,CA=7,AD为内角平分线,以AD为弦作一圆.该圆与BC相切,与AB交于M,与AC交于N,则BM+CN=4.
如图,在△ABC中,已知AB=9,BC=8,CA=7,AD为内角平分线,以AD为弦作一圆.该圆与BC相切,与AB交于M,与AC交于N,则BM+CN=4.
分析 利用面积方法证明:AB:AC=BD:DC,从而可求得BD、和DC的长,然后利用切割线定理可求得BM、CN的长,从而可求得MB+CN=4.
解答 解:过点D作DE⊥AB,垂足为E,过点D作DG⊥AC,垂足为G.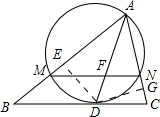
∵AD是∠BAC的平分线,DED⊥AB,DG⊥AC,
∴DE=DG.
∴△ABD与△ADC的面积比=AB:AC=9:7.
又∵△ABD与△ADC的面积比=BD:DC.
∴BD:DC=9:7.
又∵BD+DC=8,
∴BD=$\frac{9}{2}$,DC=$\frac{7}{2}$.
由切割线定理可知:MB=$\frac{B{D}^{2}}{AB}=\frac{\frac{81}{4}}{9}$=$\frac{9}{4}$,NC=$\frac{D{C}^{2}}{AC}$=$\frac{\frac{49}{4}}{7}$=$\frac{7}{4}$.
∴MB+CN=$\frac{9}{4}+\frac{7}{4}$=$\frac{16}{4}$=4.
故答案为:4.
点评 本题主要考查的是角平分线的性质、切割线定理的应用,利用面积法得到BD:DC=9:7是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列各组运算结果符号为负的有( )
①(+$\frac{3}{5}$)+(-$\frac{4}{5}$);②(-$\frac{6}{7}$)-(-$\frac{5}{6}$);③-4×0;④2×(-3)
①(+$\frac{3}{5}$)+(-$\frac{4}{5}$);②(-$\frac{6}{7}$)-(-$\frac{5}{6}$);③-4×0;④2×(-3)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.下列说法正确的是( )
| A. | 面积相等的两个三角形全等 | B. | 周长相等的两个三角形全等 | ||
| C. | 形状相同的两个三角形全等 | D. | 成轴对称的两个三角形全等 |
19.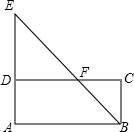 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{BC}$=$\frac{EF}{FB}$ | B. | $\frac{DE}{AD}$=$\frac{DF}{AB}$ | C. | $\frac{BC}{DE}$=$\frac{CF}{DF}$ | D. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ |
6.因为$\frac{3}{4}$a=1,所以( )
| A. | $\frac{3}{4}$是倒数 | B. | a是倒数 | C. | $\frac{3}{4}$和a都是倒数 | D. | $\frac{3}{4}$和a互为倒数 |
1.若有理数a满足a-|a|=2a,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |