题目内容
17. 已知:如图,在正方形ABCD外取-点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.
已知:如图,在正方形ABCD外取-点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.(1)求证:△APD≌△AEB;
(2)连接PC,求线段PC的长度;
(3)试求正方形ABCD的面积.
分析 (1)由四边形ABCD是正方形,得到AB=AD,∠BAD=90°,由AE⊥AP,得到∠EAP=90°,于是得到∠EAB=∠DAP,即可得到结论;
(2)连接PB,PC,由(1)证得△APD≌△AEB,于是得到PD=AE,∠ADO=∠ABE,推出△ABP≌△DCP,得到PB=PC,根据勾股定理即可得到结论;
(3)过A作AM⊥PE于M,根据等腰直角三角形的性质得到AM=PM=$\frac{1}{2}$PE=$\frac{\sqrt{2}}{2}$,求出DM=1+$\frac{\sqrt{2}}{2}$,由勾股定理得到AD=$\sqrt{(\frac{\sqrt{2}}{2})^{2}+(1+\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{2+\sqrt{2}}$,于是得到结果.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE⊥AP,
∴∠EAP=90°,
∴∠EAB=∠DAP,
在△APD与△AEB中,
$\left\{\begin{array}{l}{AE=AP}\\{∠EAB=∠DAP}\\{AB=AD}\end{array}\right.$,
∴△APD≌△AEB;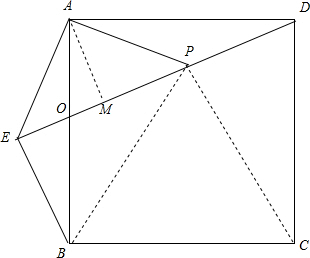
(2)连接PB,PC,由(1)证得△APD≌△AEB,
∴PD=AE,∠ADO=∠ABE,
∵AE=AP,
∴PD=AP,
∴∠PAD=∠PDA,
∴∠BAP=∠CDP,
在△ABP与△DCP中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAP=∠CDP}\\{AP=PD}\end{array}\right.$,
∴△ABP≌△DCP,
∴PB=PC,
∵∠BOE=∠AOP,
∴∠BEO=∠BAD=90°,
∵PE=$\sqrt{2}$AP=$\sqrt{2}$,
∴PB=$\sqrt{P{E}^{2}+B{E}^{2}}$=$\sqrt{3}$,
∴PC=PB=$\sqrt{3}$;
(3)过A作AM⊥PE于M,
∴AM=PM=$\frac{1}{2}$PE=$\frac{\sqrt{2}}{2}$,
∴DM=1+$\frac{\sqrt{2}}{2}$,
∴AD=$\sqrt{(\frac{\sqrt{2}}{2})^{2}+(1+\frac{\sqrt{2}}{2})^{2}}$=$\sqrt{2+\sqrt{2}}$,
∴正方形ABCD的面积=AD2=2$+\sqrt{2}$.
点评 本题考查了正方形的性质全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
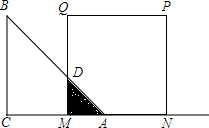 如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止.设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm.
如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止.设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm. 如图,B、C、F、E在同一直线上,AB、DE交于点G,DC=AF,∠B=∠E,∠D=∠A,
如图,B、C、F、E在同一直线上,AB、DE交于点G,DC=AF,∠B=∠E,∠D=∠A,