题目内容
5.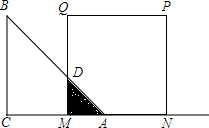 如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止.设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm.
如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止.设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm.(1)试写出y与x之间的函数表达式;
(2)当MA=4cm时,重叠部分的面积是多少?
(3)当MA的长度是多少时,等腰直角△ABC与正方形MNPQ的重叠部分以外的四边形BCMD的面积与重叠部分的面积比为3:1?
(4)开始时等腰直角△ABC中A点与M点重合,已知△ABC向右移动的速度是1cm/s,在A点与N点重合后继续向右移动,当运动停止时边BC与PN重合,探究重叠部分的面积y(cm2)与运动时间t(s)的函数表达式.
分析 (1)根据等腰直角三角形的性质和三角形的面积公式计算即可;
(2)把x=4代入解析式计算;
(3)根据相似三角形的面积比等于相似比的平方计算;
(4)分0≤x≤6和6<x≤12两种情况,根据三角形面积公式计算即可.
解答 解:(1)∵三角形ABC是等腰直角三角形,
∴MA=MD=xcm,
∴y=$\frac{1}{2}$x2;
(2)当MA=4cm时,即x=4,
y=$\frac{1}{2}$×42=8cm2;
(3)等腰直角△ABC与正方形MNPQ的重叠部分以外的四边形BCMD的面积与重叠部分的面积比为3:1,
则重叠部分的面积与等腰直角△ABC的面积比为1:4,
∴AM:AC=1:2,
∴MA=3cm;
(4)当0≤x≤6时,y=$\frac{1}{2}$x2,
当6<x≤12时,y=18-$\frac{1}{2}$(x-6)2.
点评 本题考查的是正方形和等腰直角三角形的性质,掌握等腰直角三角形的两锐角是45°是解题的关键,注意分情况讨论思想的应用.

练习册系列答案
相关题目
15.甲、乙两地相距880千米小轿车从甲地出发,2小时后,大客车从乙地出发相向而行,又经过4小时两车相遇.已知小轿车比大客车每小时多行20千米.设大客车每小时行x千米,小轿车每小时行y千米,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{x-y=20}\\{6x+4y=880}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=20}\\{6y+4x=880}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y-x=880}\\{6y+4x=20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y-x=20}\\{4y+6x=880}\end{array}\right.$ |
16.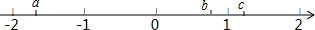 已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )
已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )
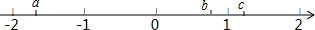 已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )
已知有理数a,b,c在数轴上的位置如图,则在-$\frac{1}{a}$,-a,c-b,c+a中,最小的一个是( )| A. | -a | B. | c-b | C. | c+a | D. | -$\frac{1}{a}$ |
 已知:如图,在正方形ABCD外取-点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.
已知:如图,在正方形ABCD外取-点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.