题目内容
3.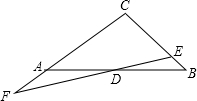 如图,△ABC中,D为边AB的中点,E为边BC上一点,ED延长线交CA延长线于点F,以下结论正确的有②④.
如图,△ABC中,D为边AB的中点,E为边BC上一点,ED延长线交CA延长线于点F,以下结论正确的有②④.①若AB=BC,BE=DE,则AF=AD;
②若∠ACB=90°,CE=DE,则AD•BD=CE•CB;
③当$\frac{BE}{CE}$=$\frac{1}{3}$时,则$\frac{FA}{AC}$=$\frac{1}{3}$;
④当$\frac{CA}{CF}$=x,$\frac{CB}{CE}$=y时,则x+y=2.
分析 ①错误.如图1中,在△ADC中,只要证明∠F<∠ADC即可说明.
②正确.如图2中,只要证明△DCE∽△BCD得$\frac{DC}{CB}$=$\frac{CE}{DC}$,再根据直角三角形斜边中线性质即可证明.
③错误.如图3中,只要证明△ADN≌△BDE,再根据$\frac{BE}{CE}$=$\frac{AN}{CE}$=$\frac{AF}{FC}$=$\frac{1}{3}$即可说明.
④正确,由如图3中,由$\frac{BE}{AE}$=$\frac{AF}{FC}$,结合条件即可证明.
解答 解:①如图1中,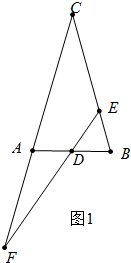 ∵BE=BD,
∵BE=BD,
∴∠BDE=∠BED=∠ADC,
∵∠BED=∠F+∠F,
∴∠F<∠BED,
∴∠F<∠ADF,
∴AD<AF,故①错误.
②如图2中,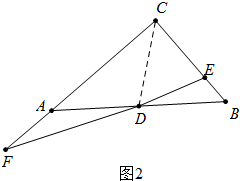
∵∠ACB=90°,AD=DB,
∴DC=AD=DB,
∴∠DCB=∠B,
∵EC=ED,
∴∠DCE=∠CDE,
∴∠CDE=∠B,∵∠DCE=∠BCD,
∴△DCE∽△BCD,
∴$\frac{DC}{CB}$=$\frac{CE}{DC}$,
∴DC2=CE•CB,
∴AD•DB=EC•CB,故②正确.
③如图3中,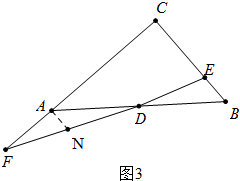
作AN∥BC交EF于N.
∵AN∥CB,
∴∠NAD=∠EBD,
在△ADN和△BDE中,
$\left\{\begin{array}{l}{∠ADN=∠BDE}\\{∠NAD=∠EBD}\\{AD=DB}\end{array}\right.$,
∴△ADN≌△BDE,
∴AN=BE,
∴$\frac{BE}{CE}$=$\frac{AN}{CE}$=$\frac{AF}{FC}$=$\frac{1}{3}$,
∴AF:AC=1:2,故③错误.
④由③可知:$\frac{BE}{CE}$=$\frac{AF}{FC}$,
∵$\frac{CA}{CF}$=x,$\frac{CB}{CE}$=y,
∴$\frac{y-1}{1}$=$\frac{1-x}{1}$,
∴x+y=2,故④正确.
故答案为②④.
点评 本题考查相似三角形的判定和性质、全等三角形的判定和性质、平行线分线段成比例定理等知识,学会添加常用辅助线是解题的关键,利用全等三角形的性质,平行线分线段成比例定理解决问题,属于中考常考题型.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
| A. | 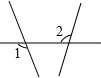 | B. | 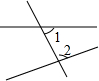 | C. |  | D. | 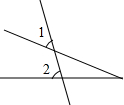 |
 直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P.
直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P. 如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.
如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.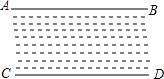 如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.
如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.