题目内容

14．如图，AD是⊙O的直径，△ABC是⊙O的内接三角形，已知AC=BC，∠DAB=50°，则∠ABC=70°．

分析 连接BD，由AD是⊙O的直径，得到∠ABD=90°，根据三角形的内角和得到∠D=40°，根据圆周角定理得到∠C=∠D=40°，由等腰直角三角形的性质即可得到结论．

解答 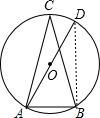解：连接BD，
∵AD是⊙O的直径，
∴∠ABD=90°，
∵∠DAB=50°，
∴∠D=40°，
∴∠C=∠D=40°，
∵AC=BC，
∴$∠ABC=\frac{1}{2}$（180°-40°）=70°，
故答案为：70．

点评 此题考查了圆周角定理，以及三角形的内角和定理，等腰三角形的性质，连接BD，构造直径所对的圆周角是解本题的关键．

练习册系列答案
相关题目
4．设一列数a1、a2、a3、…a2015、a2016中任意三个相邻数之和都是36，已知a4=2x，a5=15，a6=3+x，那么x=6，a2016=9．
5．1805年，法军在拿破仑的率领下与德军在莱茵河畔激战．德军在莱茵河北岸Q处，如图所示，因不知河宽，法军很难瞄准敌军，聪明的拿破仑站在南岸的点O处调整好自己的帽子，使视线恰好擦着帽舌边缘看到敌军兵营Q处，然后后退到B点，这是他的视点恰好能落在0处，于是他命令部下测量他脚站的B处与0点之间的距离，并下令按这个距离炮轰敌营，法军能命中目标吗？请说明理由．
2．下列计算正确的是（　　）
A．a+a2=a3B．a2•a3=a6C．（2a2）3=2a6D．a3÷a=a2
9．先化简，再求代数式的值：
（xy-2xy2）-（-3x2y2+2xy）-（3xy-2xy2），其中x=$\frac{2}{3}$，y=-2．
19．“x减去y不大于-4”用不等式可表示为x-y≤-4．
6．阅读材料：
我们知道|x|=$\left\{\begin{array}{l}{x（x＞0）}\\{0（x=0）}\\{-x（x＜0）}\end{array}\right.$，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x-2|时，可令x+1=0和x-2=0，分别求得x=-1，x=2（称-1，2分别为|x+1|与|x-2|的零点值），在实数范围内，零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况：
（1）当x＜-1时，原式=-（x+1）-（x-2）=-2x+1；
（2）当-1≤x＜2时，原式=x+1-（x-2）=3；
（3）当x≥2时，原式=x+1+x-2=2x-1．综上所述，原式=$\left\{\begin{array}{l}{-2x+1（x＜-1）}\\{3（-1≤x＜2）}\\{2x-1（x≥2）}\end{array}\right.$
学以致用：
（Ⅰ）分别求出|x+3|和|x-1|的零点值；
（Ⅱ）化简代数式|x+3|+|x-1|； 
拓展应用：
（Ⅲ）求函数y=|x+3|+|x-1|（-3≤x≤3）的最大值和最小值．
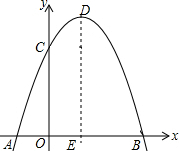3．如图，过点A（-1，0）、B（3，0）的抛物线y=-x2+bx+c与y轴交于点C，它的对称轴与x轴交于点E．
（1）求抛物线解析式；
（2）求抛物线顶点D的坐标；
（3）若抛物线的对称轴上存在点P使S△PCB=3S△POC，求此时DP的长．
4．一书的页码是连续自然数1，2，3，4，5，…规定：前30页不加进去，当从第31页开始，将页码加起来的时候，某个页码加了两次，得出的结果是2015，则这个被加了两次的页码是（　　）
A．67B．65C．63D．61

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网