Question

3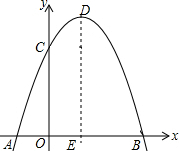．如图，过点A（-1，0）、B（3，0）的抛物线y=-x²+bx+c与y轴交于点C，它的对称轴与x轴交于点E．
（1）求抛物线解析式；
（2）求抛物线顶点D的坐标；
（3）若抛物线的对称轴上存在点P使S_△PCB=3S_△POC，求此时DP的长．

Answer 1

分析 （1）利用待定系数法即可求得解析式；
（2）把抛物线解析式化成顶点式，即可得出顶点坐标；
（3）求出△POC的面积，由三角形的面积关系得出PF=3，求出直线BC的解析式，得出F的坐标，再分两种情况讨论，即可得出DP的长．

解答 解：（1）将A（-1，0），B（3，0）代入y=-x²+bx+c得：$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$，
解得：b=2，c=3，
∴抛物线解析式为y=-x²+2x+3；
（2）∵y=-x²+2x+3=-（x-1）²+4，
∴顶点D的坐标为（1，4）；
（3）设BC与抛物线的对称轴交于点F，如图所示：
则点F的横坐标为1，
∵y=-x²+2x+3，
当x=0时，y=3，
∴OC=3，
∴△POC的面积=$\frac{1}{2}$×3×1=$\frac{3}{2}$，
∵△PCB的面积=△PCF的面积+△PBF的面积=$\frac{1}{2}$PF（1+2）=3×$\frac{3}{2}$，
解得：PF=3，
设直线BC的解析式为y=kx+a，则$\left\{\begin{array}{l}{a=3}\\{3k+a=0}\end{array}\right.$，
解得：a=3，k=-1，
∴直线BC的解析式为y=-x+3，
当x=1时，y=2，
∴F的坐标为（1，2），
∴EF=2，
当点P在F的上方时，PE=PF+EF=5，
∴DP=5-4=1；
当点P在F的下方时，PE=PF-EF=3-2=1，
∴DP=4+1=5；
综上所述：DP的长为1或5．

点评 本题考查了待定系数法求抛物线和直线的解析式；求出抛物线的顶点坐标和与y的交点坐标是本题的关键．