题目内容
4.设一列数a1、a2、a3、…a2015、a2016中任意三个相邻数之和都是36,已知a4=2x,a5=15,a6=3+x,那么x=6,a2016=9.分析 由a4+a5+a6=36,可得出关于x的一元一次方程,解方程即可得出x的值;由该数列中任意三个相邻数之和都是36,可找出数的变化规律“a3n+1=12,a3n+2=15,a3n+3=9(n为自然数)”,依此规律即可得出结论.
解答 解:由已知得:a4+a5+a6=36,即2x+15+3+x=36,
解得:x=6.
∴a4=12,a5=15,a6=9,
∵该数列中任意三个相邻数之和都是36,
∴a3n+1=12,a3n+2=15,a3n+3=9(n为自然数).
∵2016=3×672,
∴a2016=9.
故答案为:6;9.
点评 本题考查了规律型中的数字的变化,解题的关键是找出数的变化规律“a3n+1=12,a3n+2=15,a3n+3=9(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,根据数列中数的变化找出变化规律是关键.

练习册系列答案
相关题目
15.已知a=$\sqrt{5}$+$\sqrt{3}$,b=$\frac{2}{\sqrt{5}-\sqrt{3}}$,则a与b的关系是( )
| A. | a=b | B. | ab=1 | C. | a=-b | D. | ab=-5 |
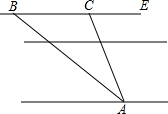 在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)

 如图,AD是⊙O的直径,△ABC是⊙O的内接三角形,已知AC=BC,∠DAB=50°,则∠ABC=70°.
如图,AD是⊙O的直径,△ABC是⊙O的内接三角形,已知AC=BC,∠DAB=50°,则∠ABC=70°.