在下列网格中.小正方形的边长为1.点A.B.O都在格点上.则∠A的正弦值是( )A．$\frac{\sqrt{5}}{5}$B．$\frac{\sqrt{5}}{10}$C．$\frac{2\sqrt{5}}{5}$D．$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

14．

在下列网格中，小正方形的边长为1，点A、B、O都在格点上，则∠A的正弦值是（　　）

A．

$\frac{\sqrt{5}}{5}$

B．

$\frac{\sqrt{5}}{10}$

C．

$\frac{2\sqrt{5}}{5}$

D．

$\frac{1}{2}$

分析根据勾股定理求出OA，根据正弦的定义解答即可．

解答解：由题意得，OC=2，AC=4，
由勾股定理得，AO=$\sqrt{A{C}^{2}+O{C}^{2}}$=2$\sqrt{5}$，
∴sinA=$\frac{OC}{OA}$=$\frac{\sqrt{5}}{5}$，
故选：A．

点评本题考查的是锐角三角函数的定义，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

练习册系列答案

开心快乐假期作业寒假作业西安出版社系列答案

名题教辅寒假作业快乐衔接武汉出版社系列答案

走进名校天府中考一本通系列答案

QQ教辅中考题库系列答案

小考必备小升初三年真题测试卷系列答案

相关题目

4．

如图，点A、B、C在同一直线上，H为AC的中点，M为AB的中点，N为BC的中点，则下列说法：①MN=HC；②MH=$\frac{1}{2}$（AH-HB）；③MN=$\frac{1}{2}$（AC+HB）；④HN=$\frac{1}{2}$（HC+HB），其中正确的是（　　）

5．

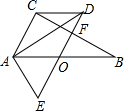如图，已知Rt△ABC中，∠C=90°，∠B=30°，O为AB边中点，将△ABC绕点O逆时针旋转60°至△EDA位置，连接CD．
（1）求证：OD⊥BC；
（2）求证：四边形AODC为菱形．

2．

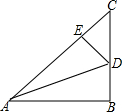如图，在△ABC中，∠B=90°，AB=BC=4，点D在BC上，将△ABC沿AD折叠，使点B落在AC边上的点E处．
（1）判断△CDE是什么特殊三角形，并说明理由；
（2）求线段BD的长．

9．若抛物线y=x²-bx+9的顶点在x轴的负半轴上，则b的值为（　　）

19．

如图，一观测塔底座部分是四棱柱，现在从下底面A点修建钢筋扶梯，经过点M、N到点D′，再进入顶部的观测室，已知AB=BC=CD=3米，高AA′=9米，问点M、N位于什么位置，才能使扶梯的总长度最小，从而造价最低？

6．己知代数式2y²+3y+7的值是8，则代数式4y²+6y-9的值是（　　）

3．利群超市经销某品牌童装，单价为每件40元时，每天销量为60件，当从单价每件40元降了20元时，一天销量为100件，设降x元时，一天的销量为y千克．已知y是x的一次函数．
（1）求y与x之间的关系式；
（2）若某天销售童装80件，则该天童装的单价是多少？

4．【现场学习】
定义：我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”．
如：|x|=2，|2x-1|=3，|${\frac{x-1}{2}}$|-x=1，…都是含有绝对值的方程．
怎样求含有绝对值的方程的解呢？基本思路是：含有绝对值的方程→不含有绝对值的方程．
我们知道，根据绝对值的意义，由|x|=2，可得x=2或x=-2．
[例]解方程：|2x-1|=3．
我们只要把2x-1看成一个整体就可以根据绝对值的意义进一步解决问题．
解：根据绝对值的意义，得2x-1=3或2x-1=-3．
解这两个一元一次方程，得x=2或x=-1．
检验：
（1）当x=2时，
原方程的左边=|2x-1|=|2×2-1|=3，
原方程的右边=3，
∵左边=右边
∴x=2是原方程的解．
（2）当x=-1时，
原方程的左边=|2x-1|=|2×（-1）-1|=3，
原方程的右边=3，
∵左边=右边
∴x=-1是原方程的解．
综合（1）（2）可知，原方程的解是：x=2，x=-1．
【解决问题】
解方程：|${\frac{x-1}{2}}$|-x=1．

试题分类