题目内容
10．
如图，在△ABC中，AD=BD，AD⊥BC于点D，∠C=55°，求∠BAC的度数．
分析 根据垂直的定义可得∠ADB=∠ADC=90°，再根据直角三角形两锐角互余求出∠CAD，然后求出∠BAD，再求解即可．
解答 解：∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∵∠C=55°，
∴∠CAD=90°-∠C=90°-55°=35°，
∵AD=BD，
∴∠BAD=∠B=45°，
∴∠BAC=∠BAD+∠DAC=45°+35°=80°．
点评 本题考查了直角三角形两锐角互余的性质，等腰直角三角形的性质，是基础题，熟记性质并准确识图是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
20．
如图，平面直角坐标系中，矩形ABCO与双曲线y=$\frac{k}{x}$（x＞0）交于D、E两点，将△OCD沿OD翻折，点C的对称点C′恰好落在边AB上，已知OA=3，OC=5，则AE长为（ ）
如图，平面直角坐标系中，矩形ABCO与双曲线y=$\frac{k}{x}$（x＞0）交于D、E两点，将△OCD沿OD翻折，点C的对称点C′恰好落在边AB上，已知OA=3，OC=5，则AE长为（ ）| A． | 4 | B． | 3 | C． | $\frac{26}{9}$ | D． | $\frac{25}{9}$ |
1．
如图，直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处，那么，下列结论中错误的是（ ）
如图，直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处，那么，下列结论中错误的是（ ）| A． | AC=DF | B． | ∠DEF=90° | C． | △ABC≌△DEF | D． | EC=CF |
18．在平面直角坐标系中，将点A（-1，4）向右平移2个单位长度，再向上平移3个单位长度，则平移后对应点的坐标是（ ）
| A． | （1，7） | B． | （1，1） | C． | （-3，7） | D． | （-3，1） |
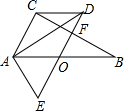如图，已知Rt△ABC中，∠C=90°，∠B=30°，O为AB边中点，将△ABC绕点O逆时针旋转60°至△EDA位置，连接CD．
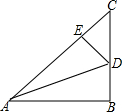如图，在△ABC中，∠B=90°，AB=BC=4，点D在BC上，将△ABC沿AD折叠，使点B落在AC边上的点E处．
如图，一观测塔底座部分是四棱柱，现在从下底面A点修建钢筋扶梯，经过点M、N到点D′，再进入顶部的观测室，已知AB=BC=CD=3米，高AA′=9米，问点M、N位于什么位置，才能使扶梯的总长度最小，从而造价最低？
某地区随机抽查了一部分市民进行法律知识测试，测试成绩（得分取整数，每组数据含最小值不含最大值）整理后，得到如图所示的频数分布直方图，写出一条你从图中所获得的信息：分数在70～80之间的人数最多；成绩低于60分的有3人；成绩90分及其以上的有6人；参加测试的共有48人等．