题目内容
13. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=4,求BC的长.
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=4,求BC的长.
分析 根据等边三角形性质求出OA=OB=AB=4,根据平行四边形的性质求出OA=OC,OB=OD,得出AC=BD=8,证出四边形ABCD是矩形,得出∠ABC=90°,由勾股定理求出BC即可.
解答 解:∵△ABO是等边三角形,
∴OA=OB=AB=4,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴OA=OC=OB=OD,
∴AC=BD=8,
∴四边形ABCD是矩形,
∴∠ABC=90°,
由勾股定理得:BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$.
点评 本题考查了等边三角形的性质、平行四边形的性质,勾股定理,矩形的判定与性质;熟练掌握平行四边形和等边三角形的性质,证明四边形是矩形是解决问题的关键.

练习册系列答案
相关题目
4. 如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=$\frac{1}{2}$(AH-HB);③MN=$\frac{1}{2}$(AC+HB);④HN=$\frac{1}{2}$(HC+HB),其中正确的是( )
如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=$\frac{1}{2}$(AH-HB);③MN=$\frac{1}{2}$(AC+HB);④HN=$\frac{1}{2}$(HC+HB),其中正确的是( )
 如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=$\frac{1}{2}$(AH-HB);③MN=$\frac{1}{2}$(AC+HB);④HN=$\frac{1}{2}$(HC+HB),其中正确的是( )
如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=$\frac{1}{2}$(AH-HB);③MN=$\frac{1}{2}$(AC+HB);④HN=$\frac{1}{2}$(HC+HB),其中正确的是( )| A. | ①② | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
1. 如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )
如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )
 如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )
如图,直角三角形ABC沿直角边BC所在的直线向右平移到△DEF处,那么,下列结论中错误的是( )| A. | AC=DF | B. | ∠DEF=90° | C. | △ABC≌△DEF | D. | EC=CF |
18.在平面直角坐标系中,将点A(-1,4)向右平移2个单位长度,再向上平移3个单位长度,则平移后对应点的坐标是( )
| A. | (1,7) | B. | (1,1) | C. | (-3,7) | D. | (-3,1) |
 如图,已知四点A、B、C、D,根据下列语句,画出图形.
如图,已知四点A、B、C、D,根据下列语句,画出图形.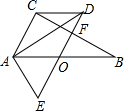 如图,已知Rt△ABC中,∠C=90°,∠B=30°,O为AB边中点,将△ABC绕点O逆时针旋转60°至△EDA位置,连接CD.
如图,已知Rt△ABC中,∠C=90°,∠B=30°,O为AB边中点,将△ABC绕点O逆时针旋转60°至△EDA位置,连接CD.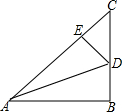 如图,在△ABC中,∠B=90°,AB=BC=4,点D在BC上,将△ABC沿AD折叠,使点B落在AC边上的点E处.
如图,在△ABC中,∠B=90°,AB=BC=4,点D在BC上,将△ABC沿AD折叠,使点B落在AC边上的点E处.