题目内容
17.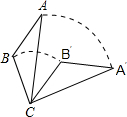 如图,将△ABC绕点C旋转60°得到△A′B′C,已知AC=6,BC=2$\sqrt{5}$,则线段AB扫过的图形的面积为( )
如图,将△ABC绕点C旋转60°得到△A′B′C,已知AC=6,BC=2$\sqrt{5}$,则线段AB扫过的图形的面积为( )| A. | π | B. | 3π | C. | 6π | D. | $\frac{8}{3}$π |
分析 根据图形可以得出AB扫过的图形的面积=S扇形ACA′+S△ABC-S扇形BCB′-S△A′B′C,由旋转的性质就可以得出S△ABC=S△A′B′C就可以得出AB扫过的图形的面积=S扇形ACA′-S扇形BCB′求出其值即可.
解答 解:∵△ABC绕点C旋转60°得到△A′B′C,
∴△ABC≌△A′B′C,
∴S△ABC=S△A′B′C,∠BCB′=∠ACA′=60°.
∵AB扫过的图形的面积=S扇形ACA′+S△ABC-S扇形BCB′-S△A′B′C,
∴AB扫过的图形的面积=S扇形ACA′-S扇形BCB′,
∴AB扫过的图形的面积=$\frac{60π×{6}^{2}}{360}$-$\frac{60π×(2\sqrt{5})^{2}}{360}$=6π-$\frac{10}{3}$π=$\frac{8}{3}$π.
故选:D.
点评 本题考查了旋转的性质的运用,全等三角形的性质的运用,扇形的面积公式的运用,根据旋转的性质把问题转化是解决问题的关键.

练习册系列答案
相关题目
5.若(xm)n÷B=xmn,则B等于( )
| A. | xm | B. | xn | C. | 1 | D. | xmn |
12.下列条件能让两个三角形全等的是( )
| A. | 有一边和两角对应相等 | B. | 有两边和一角对应相等 | ||
| C. | 三个角对应相等 | D. | 面积相等且有一边相等 |
2.若分式$\frac{3x+3y}{xy}$中,x、y的值都变为原来的3倍,则分式的值( )
| A. | 不变 | B. | 变为原来的3倍 | C. | 变为原来的$\frac{1}{3}$ | D. | 变为原来的$\frac{1}{6}$ |
 如图所示的圆柱体,它的底面半径为2cm,高为6cm.
如图所示的圆柱体,它的底面半径为2cm,高为6cm.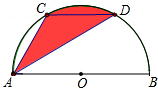 如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.
如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.