题目内容
7．
如图所示的圆柱体，它的底面半径为2cm，高为6cm．（1）想一想：该圆柱体的截面有几种不同形状的平面图形？
（2）议一议：你能截出截面最大的长方形吗？
（3）算一算：截得的长方形面积的最大值为多少？
分析 （1）根据圆柱几何体的形状特点和截面的角度判断即可．
（2）根据题意可得出截面面积最大是长方形，依此即可求解；
（3）根据长方形的面积公式即可得出答案．
解答 解：（1）该圆柱体的截面有三种，平行轴线截切，截面是矩形，垂直轴线截切，截面是圆，倾斜轴线截切，截面是椭圆；
（2）根据题意可得：截面面积最大是长方形，并且长是6cm，宽是4cm，
（3）截面面积最大是6×4=24（cm2）．
故截得的长方形面积的最大值为24cm2．
点评 此题考查了截一个几何体，根据截面的形状既与被截的几何体有关，还与截面的角度和方向有关，得出这个圆柱体的截面面积最大是长方形是本题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
17．已知⊙O的半径为5cm，直线L上有一点P到圆心距离等于5，则直线L与⊙O的位置关系为（ ）
| A． | 相交 | B． | 相离 | C． | 相切 | D． | 相交或相切 |
18．使式子$\sqrt{-{x}^{2}}$有意义的x是（ ）
| A． | 全体正数 | B． | 全体负数 | C． | 零 | D． | 非零数 |
15．解下列分式方程
（1）$\frac{3}{2x-2}+\frac{1}{1-x}=3$
（2）$\frac{1}{x+3}-\frac{2}{3-x}=\frac{12}{{x}^{2}-9}$．
（1）$\frac{3}{2x-2}+\frac{1}{1-x}=3$
（2）$\frac{1}{x+3}-\frac{2}{3-x}=\frac{12}{{x}^{2}-9}$．
19．
如图，抛物线y=ax2+bx+c交x轴于（-1，0），（2，0），则下列结论：①ac＞0；②a+b=0；③当x$＜\frac{1}{4}$时，y随x的增大而增大；④a-b+c＜0．其中正确的个数有（ ）
如图，抛物线y=ax2+bx+c交x轴于（-1，0），（2，0），则下列结论：①ac＞0；②a+b=0；③当x$＜\frac{1}{4}$时，y随x的增大而增大；④a-b+c＜0．其中正确的个数有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
16．据阿里巴巴实时数据显示，2015天猫双十一全球狂欢节最终以912.17亿元交易额拉下帷幕．将数字912.17亿精确到1亿，并用科学记数法表示约为（ ）
| A． | 912×108 | B． | 9.12×109 | C． | 9.12×1010 | D． | 0.912×1011 |
17．
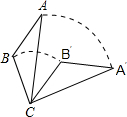如图，将△ABC绕点C旋转60°得到△A′B′C，已知AC=6，BC=2$\sqrt{5}$，则线段AB扫过的图形的面积为（ ）
如图，将△ABC绕点C旋转60°得到△A′B′C，已知AC=6，BC=2$\sqrt{5}$，则线段AB扫过的图形的面积为（ ）| A． | π | B． | 3π | C． | 6π | D． | $\frac{8}{3}$π |