题目内容
8.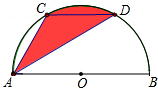 如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.
如图,已知AB为半圆O的直径,弦CD=8厘米,CD∥AB,∠CAD=30°,则图中阴影部分的面积等于$\frac{32π}{3}$平方厘米.
分析 连接OC,OD,判断出阴影部分的面积=扇形OCD的面积,根据扇形的面积公式即可求解.
解答 解:如图,
连接OC,OD,
∵∠CAD=30°,
∴∠COD=60°,
∵AB∥CD,
∴△ACD的面积=△COD的面积,
∴阴影部分的面积=弓形CD的面积+△COD的面积=扇形OCD的面积=$\frac{60π×{8}^{2}}{360}$=$\frac{32π}{3}$平方厘米.
故答案为:$\frac{32π}{3}$.
点评 此题考查了扇形的面积公式,利用等底等高三角形的面积相等,把阴影部分的面积转化为扇形COD的面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.使式子$\sqrt{-{x}^{2}}$有意义的x是( )
| A. | 全体正数 | B. | 全体负数 | C. | 零 | D. | 非零数 |
19. 如图,抛物线y=ax2+bx+c交x轴于(-1,0),(2,0),则下列结论:①ac>0;②a+b=0;③当x$<\frac{1}{4}$时,y随x的增大而增大;④a-b+c<0.其中正确的个数有( )
如图,抛物线y=ax2+bx+c交x轴于(-1,0),(2,0),则下列结论:①ac>0;②a+b=0;③当x$<\frac{1}{4}$时,y随x的增大而增大;④a-b+c<0.其中正确的个数有( )
 如图,抛物线y=ax2+bx+c交x轴于(-1,0),(2,0),则下列结论:①ac>0;②a+b=0;③当x$<\frac{1}{4}$时,y随x的增大而增大;④a-b+c<0.其中正确的个数有( )
如图,抛物线y=ax2+bx+c交x轴于(-1,0),(2,0),则下列结论:①ac>0;②a+b=0;③当x$<\frac{1}{4}$时,y随x的增大而增大;④a-b+c<0.其中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.据阿里巴巴实时数据显示,2015天猫双十一全球狂欢节最终以912.17亿元交易额拉下帷幕.将数字912.17亿精确到1亿,并用科学记数法表示约为( )
| A. | 912×108 | B. | 9.12×109 | C. | 9.12×1010 | D. | 0.912×1011 |
13.已知a<0,那么点(3-a,-a2-3)关于y轴的对称点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.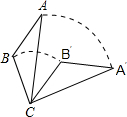 如图,将△ABC绕点C旋转60°得到△A′B′C,已知AC=6,BC=2$\sqrt{5}$,则线段AB扫过的图形的面积为( )
如图,将△ABC绕点C旋转60°得到△A′B′C,已知AC=6,BC=2$\sqrt{5}$,则线段AB扫过的图形的面积为( )
 如图,将△ABC绕点C旋转60°得到△A′B′C,已知AC=6,BC=2$\sqrt{5}$,则线段AB扫过的图形的面积为( )
如图,将△ABC绕点C旋转60°得到△A′B′C,已知AC=6,BC=2$\sqrt{5}$,则线段AB扫过的图形的面积为( )| A. | π | B. | 3π | C. | 6π | D. | $\frac{8}{3}$π |
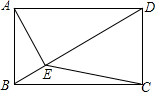 如图,在矩形ABCD中,BC=4,AE⊥BD于E,若∠BAE=30°,则S△ECD=2$\sqrt{3}$.
如图,在矩形ABCD中,BC=4,AE⊥BD于E,若∠BAE=30°,则S△ECD=2$\sqrt{3}$.