若分式$\frac{3x+3y}{xy}$中.x.y的值都变为原来的3倍.则分式的值( )A．不变B．变为原来的3倍C．变为原来的$\frac{1}{3}$D．变为原来的$\frac{1}{6}$ 题目和参考答案——青夏教育精英家教网—

题目内容

2．若分式$\frac{3x+3y}{xy}$中，x、y的值都变为原来的3倍，则分式的值（　　）

A．

不变

B．

变为原来的3倍

C．

变为原来的$\frac{1}{3}$

D．

变为原来的$\frac{1}{6}$

分析根据分式的基本性质，即可解答．

解答解：$\frac{3x+3y}{xy}$=$\frac{3×3x+3×3y}{3x×3y}=\frac{3（3x+3y）}{9xy}=\frac{3x+3y}{3xy}$=$\frac{1}{3}×\frac{3x+3y}{xy}$，
所以变为原来的$\frac{1}{3}$．
故选：C．

点评本题主要考查了分式的基本性质，在解题时要注意对基本性质灵活应用是本题的关键．

练习册系列答案

相关题目

12．若2a+3b+2=0，则9^a×27^b=$\frac{1}{9}$．

13．已知a＜0，那么点（3-a，-a²-3）关于y轴的对称点在（　　）

10．已知a²+3ab=7，2ab+5b²=4，则a²+5ab+5b²=11．

17．

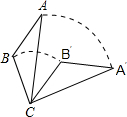如图，将△ABC绕点C旋转60°得到△A′B′C，已知AC=6，BC=2$\sqrt{5}$，则线段AB扫过的图形的面积为（　　）

7．关于x的方程2x+m=1-x的解是x=-2，则m的值为7．

14．解方程
（1）-3+3x=2x
（2）4（2x+1）=-1
（3）4-3（2-x）=5x
（4）2-$\frac{x+5}{6}$=x-$\frac{x-1}{3}$．

11．在平面直角坐标系中，点A（-4，3）关于原点的对称点的坐标为（　　）

a³•a²=a⁵

a⁶÷a³=a²

试题分类