题目内容
10.为了防控甲型H1N1流感,某校积极进行校园的环境消毒,为此购买了甲、乙两种消毒液,现已知过去两次购买这两种消毒液的瓶数和总费用如表所示:| 甲种消毒液(瓶) | 乙种消毒液(瓶) | 总费用(元) | |
| 第一次 | 40 | 60 | 660 |
| 第二次 | 80 | 30 | 690 |
(2)现在学校决定购买甲乙两种消毒液共300瓶,要求甲乙两种的数量都不少于100瓶,并且甲的数量不少于乙数量的$\frac{3}{2}$,请你帮助学校计算购买时最低费用为多少?
分析 (1)设每瓶甲种消毒液的每瓶的价格是x元,每瓶乙种消毒液的价格是y元,根据题意列方程求解;
(2)根据题意列不等式求解即可.
解答 解:(1)设甲种消毒液为x元,乙种消毒液为y元.
由题意列方程组得:$\left\{\begin{array}{l}{40x+60y=660}\\{80x+30y=690}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$,
答:甲种消毒每瓶6元,乙种消毒液每瓶9元;
(2)设甲a瓶,则乙( 300-a )瓶根据题意可得$\left\{\begin{array}{l}{a≥100}\\{300-a≥100}\\{a≥\frac{3}{2}(300-a)}\end{array}\right.$得180≤a≤200,
所以w总=6a+7( 300-a )=-a+2100,
所以当a=200时有最低费用1900元.
点评 此题主要考查了二元一次方程组和一元一次不等式的应用,关键是正确理解题意,设出合适的未知数,找出题目中的不等关系,列出不等式.

练习册系列答案
相关题目
8.一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
| 销售方式 | 粗加工后销售 | 精加工后销售 |
| 每吨获利(元) | 1000 | 2000 |
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
1.x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,则(1+$\frac{1}{y}$)(1-$\frac{1}{x}$)=( )
| A. | $4\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{3}{2}$ |
15.如果$\sqrt{\frac{x}{x-3}}=\frac{\sqrt{x}}{\sqrt{x-3}}$成立,那么( )
| A. | x≥3 | B. | 0≤x≤3 | C. | x≥0 | D. | x>3 |
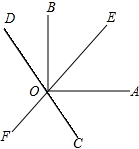 如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.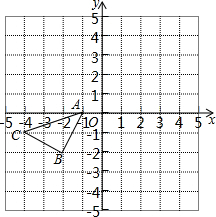 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: 如图,在⊙O中,∠C=30°,AB=2cm,则弧AB的长等于$\frac{2π}{3}$.(结果保留π)
如图,在⊙O中,∠C=30°,AB=2cm,则弧AB的长等于$\frac{2π}{3}$.(结果保留π)