题目内容
 在一直角三角形的两直角边上各取一点,分别沿斜边中线与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,其中三边长分别为3、4、4,则原直角三角形的斜边长是( )
在一直角三角形的两直角边上各取一点,分别沿斜边中线与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,其中三边长分别为3、4、4,则原直角三角形的斜边长是( )| A、10 | ||
B、8
| ||
C、10或8
| ||
D、10或4
|
考点:直角梯形,勾股定理,图形的剪拼
专题:
分析:先根据题意画出图形,再根据勾股定理求出斜边上的中线,最后即可求出斜边的长.
解答:解:分为两种情况:
①如图:

延长CE到A,延长CF到B,连接AB,使AB过D,且D为AB的中点,连接CD,
在Rt△CED中,DE=3,EC=4,由勾股定理得:CD=
=5,
则AB=2CD=10;
②如图:

延长EC到A,延长ED到B,连接AB,使AB过F,且F为AB的中点,连接EF,
在Rt△ECF中,CE=4,CF=4,由勾股定理得:EF=
=4
,
则AB=2CD=8
;
故选C.
①如图:

延长CE到A,延长CF到B,连接AB,使AB过D,且D为AB的中点,连接CD,
在Rt△CED中,DE=3,EC=4,由勾股定理得:CD=
| 32+42 |
则AB=2CD=10;
②如图:

延长EC到A,延长ED到B,连接AB,使AB过F,且F为AB的中点,连接EF,
在Rt△ECF中,CE=4,CF=4,由勾股定理得:EF=
| 42+42 |
| 2 |
则AB=2CD=8
| 2 |
故选C.
点评:此题考查了图形的剪拼,解题的关键是能够根据题意画出图形,在解题时要注意分两种情况画图,不要漏解.

练习册系列答案
相关题目
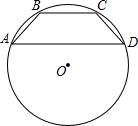 已知⊙O的半径为4,A,B,C,D是圆上的四个点,且AB=BC=CD=2,那么AD的长为( )
已知⊙O的半径为4,A,B,C,D是圆上的四个点,且AB=BC=CD=2,那么AD的长为( )A、2
| ||
| B、5.5 | ||
C、2
| ||
| D、5.4 |
若函数y=
(k为非零常数)的图象在第二、四象限内,则函数y=kx2+x-2的图象在( )
| k |
| x |
A、直线y=-
| ||
B、直线y=-
| ||
C、直线x=-
| ||
D、直线x=-
|
在平面直角坐标系中,若点P(x-2,x)在x轴上,则点P的坐标为( )
| A、(0,-2) |
| B、(0,2) |
| C、(-2,0) |
| D、(2,0) |
 如图,直角坐标系中,在第一象限AB方向和x轴上个有一平面镜,一束光从OB上的C点射出,经AB上的D点反射到x轴上的E点后沿EF反射出去,∠DCE>∠DEC.(物理实验告诉我们,光的反射过程中,入射角等于反射角,数学上的理解如图中∠ADE=∠BDC)
如图,直角坐标系中,在第一象限AB方向和x轴上个有一平面镜,一束光从OB上的C点射出,经AB上的D点反射到x轴上的E点后沿EF反射出去,∠DCE>∠DEC.(物理实验告诉我们,光的反射过程中,入射角等于反射角,数学上的理解如图中∠ADE=∠BDC) 如图,已知每个小正方形的边长均为1,A、B、C、D是小正方形的顶点,AB、CD交于点O,求∠AOC的度数.
如图,已知每个小正方形的边长均为1,A、B、C、D是小正方形的顶点,AB、CD交于点O,求∠AOC的度数. 已知,AB是⊙O的直径,半径CO⊥AB,过OC的中点H作EF∥AB,求∠EBA的度数.
已知,AB是⊙O的直径,半径CO⊥AB,过OC的中点H作EF∥AB,求∠EBA的度数.