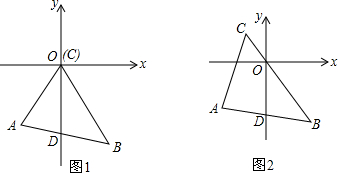题目内容
 如图,直角坐标系中,在第一象限AB方向和x轴上个有一平面镜,一束光从OB上的C点射出,经AB上的D点反射到x轴上的E点后沿EF反射出去,∠DCE>∠DEC.(物理实验告诉我们,光的反射过程中,入射角等于反射角,数学上的理解如图中∠ADE=∠BDC)
如图,直角坐标系中,在第一象限AB方向和x轴上个有一平面镜,一束光从OB上的C点射出,经AB上的D点反射到x轴上的E点后沿EF反射出去,∠DCE>∠DEC.(物理实验告诉我们,光的反射过程中,入射角等于反射角,数学上的理解如图中∠ADE=∠BDC)(1)若∠ABC=40°,DC平分∠BDE,求∠DEC的度数;
(2)如图,若∠ABE=35°,求入射光线CD与反射光线EF所在直线的夹角∠P的度数.
考点:三角形内角和定理,坐标与图形性质,三角形的外角性质
专题:
分析:(1)根据题意求得∠ADE=∠BDC=∠CDE=60°,根据三角形外角的性质即可求得∠DEC的度数;
(2)根据题意设∠ADE=∠BDC=∠β,∠DEB=∠PEB=∠α,根据三角形外角的性质得出∠β=35°+∠α,然后根据三角形内角和定理即可求得.
(2)根据题意设∠ADE=∠BDC=∠β,∠DEB=∠PEB=∠α,根据三角形外角的性质得出∠β=35°+∠α,然后根据三角形内角和定理即可求得.
解答:解:(1)∵DC平分∠BDE,
∴∠BDC=∠CDE,
∵∠ADE=∠BDC,
∴∠ADE=∠BDC=∠CDE=60°,
∵∠ADE=∠B+∠DEC,∠ABC=40°
∴∠DEC=∠ADE-∠B=60°-40°=20°.
(2)∵∠ADE=∠BDC,
设∠ADE=∠BDC=∠β,
∴∠PDE=180°-2∠β,
由于入射角等于反射角,∠PEB与反射角是对顶角,所以∠PEB=∠DEB,
∵∠ADE=∠B+∠DEB,
设∠DEB=∠PEB=∠α,
∴∠β=∠B+∠α=35°+∠α,∠PED=2∠α,
∴∠P=180°-∠PDE-∠PED=180°-180°+2∠β-2∠α=2∠β-2∠α=2(∠β-∠α)=2(35°+∠α-∠α)=70°.
∴∠BDC=∠CDE,
∵∠ADE=∠BDC,
∴∠ADE=∠BDC=∠CDE=60°,
∵∠ADE=∠B+∠DEC,∠ABC=40°
∴∠DEC=∠ADE-∠B=60°-40°=20°.
(2)∵∠ADE=∠BDC,
设∠ADE=∠BDC=∠β,
∴∠PDE=180°-2∠β,
由于入射角等于反射角,∠PEB与反射角是对顶角,所以∠PEB=∠DEB,
∵∠ADE=∠B+∠DEB,
设∠DEB=∠PEB=∠α,
∴∠β=∠B+∠α=35°+∠α,∠PED=2∠α,
∴∠P=180°-∠PDE-∠PED=180°-180°+2∠β-2∠α=2∠β-2∠α=2(∠β-∠α)=2(35°+∠α-∠α)=70°.
点评:本题考查了三角形外角的性质,三角形内角和定理,对顶角相等等,熟练掌握性质和定理,找出角之间的关系是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
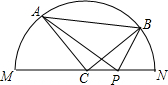 如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若
如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若 |
| MA |
 |
| BN |
| A、10° | B、15° |
| C、20° | D、25° |
泗水县龙城中学去年对实验器材的投资为2万元,预计明年的投资为8万元.若设该校今明两年在实验器材投资上年平均增长率是x,根据题意,下面所列方程正确的是( )
| A、2(1+x)2=8 |
| B、8(1+x)2=2 |
| C、2(1-x)2=8 |
| D、2+2(1+x)+2(1+x)2=8 |
 在一直角三角形的两直角边上各取一点,分别沿斜边中线与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,其中三边长分别为3、4、4,则原直角三角形的斜边长是( )
在一直角三角形的两直角边上各取一点,分别沿斜边中线与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,其中三边长分别为3、4、4,则原直角三角形的斜边长是( )| A、10 | ||
B、8
| ||
C、10或8
| ||
D、10或4
|