题目内容
1．求证：不论k取什么实数，方程x2-（k+4）x+4（k-1）=0一定有两个不相等的实数根．分析 根据方程各项系数利用根的判别式即可得出△=k2+32≥32，从而得出无论k取什么实数方程总有两个不相等的实数根．
解答 证明：在方程x2-（k+4）x+4（k-1）=0中，
△=[-（k+4）]2-4×1×4（k-1）=k2+32≥32，
∴不论k取什么实数，方程x2-（k+4）x+4（k-1）=0一定有两个不相等的实数根．
点评 本题考查了根的判别式，找出△=k2+32≥32是解题的关键．
练习册系列答案
相关题目
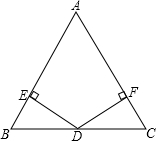已知：如图，在△ABC中，点D是BC的中点，过点D作DE⊥AB，DF⊥AC，点E，F分别为垂足，且满足BE=CF．求证：AE=AF．
如图所示，在矩形ABCD中，BC=4，AB=2，P是BC上一动点，动点Q在PC或其延长线上，BP=PQ，四边形PQRS是以PQ为一边的正方形，点P从点B开始沿射线BC方向运动，设BP=x，正方形PQRS与矩形ABCD重叠部分的面积为y．