题目内容
 (1)观察发现:
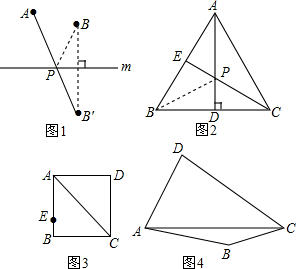
(1)观察发现:如图1,若点A、B在直线l同侧,在直线l上求作一点P,使AP+BP最小.
作法:作点B关于直线l的对称点B′,连接B′A交直线l于点P,点P即为所求.
如图2,AD是等边△ABC的高,点E是AB的中点,在AD上求作一点P,使BP+PE最小.
作法:连接CE交AD于点P,点P即为所求.若AB=2,则BP+PE的最小值为
(2)实践运用:
如图3,在正方形ABCD的边长是4,BE=1,在对角线AC上求作一点P,使BP+EP最小,并求出BP+EP的最小值;
(3)拓展延伸:
如图4,在四边形ABCD的对角线AC上求作一点P,使∠APB=∠APD.(保留作图痕迹,不必写出作法)
考点:轴对称-最短路线问题
专题:
分析:(1)由题意可知,CE的长即为BP+PE的最小值,根据等边三角形三线合一的性质可知CE⊥AB,∠BCE=∠BCA=30°,BE=1,再根据CE=
BE即可得出结论;
(2)连接BD,则点D即为点B关于AC的对称点,连接DE交AC于点P,根据两点之间线段最短可知,点P即为所求;
(3)作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P.
| 3 |
(2)连接BD,则点D即为点B关于AC的对称点,连接DE交AC于点P,根据两点之间线段最短可知,点P即为所求;
(3)作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P.
解答: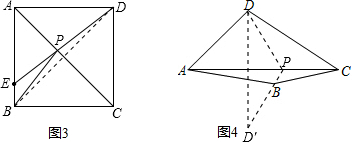 解:(1)CE的长即为BP+PE的最小值.
解:(1)CE的长即为BP+PE的最小值.
∵在等边△ABC中,AB=2,点E是AB的中点,
∴CE⊥AB,∠BCE=∠BCA=30°,BE=1,
∴CE=
BE=
.
故答案为:
;
(2)如图3,连接BD,则点D即为点B关于AC的对称点,连接DE交AC于点P,根据两点之间线段最短可知,点P即为所求.
∵正方形ABCD的边长是4,BE=1,
∵AE=3,AD=4,
∴DE=
=
=5;
(3)如图4.作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P.
 解:(1)CE的长即为BP+PE的最小值.
解:(1)CE的长即为BP+PE的最小值.∵在等边△ABC中,AB=2,点E是AB的中点,
∴CE⊥AB,∠BCE=∠BCA=30°,BE=1,
∴CE=
| 3 |
| 3 |
故答案为:
| 3 |
(2)如图3,连接BD,则点D即为点B关于AC的对称点,连接DE交AC于点P,根据两点之间线段最短可知,点P即为所求.
∵正方形ABCD的边长是4,BE=1,
∵AE=3,AD=4,
∴DE=
| AE2+AD2 |
| 32+42 |
(3)如图4.作点D关于AC的对称点D',连接D'B,并延长与AC的交点即为点P.
点评:本题考查的是轴对称-最短路线问题,熟知两点之间,线段最短是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
计算(-3a4b2)3的结果是( )
| A、-9a12b6 |
| B、-27a7b5 |
| C、9a12b6 |
| D、-27a12b6 |
若0<x<1,则x,
,x2的大小关系是( )
| 1 |
| x |
A、
| ||
B、x<
| ||
C、
| ||
D、x2<x<
|
 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积的积为( )
如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积的积为( )A、(
| ||
B、
| ||
C、
| ||
D、(
|
 如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.
如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B. 已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)
已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3) 如图,在△ABC中,
如图,在△ABC中,