题目内容
 如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.
如图,直线y=-x-2交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c的顶点为A,且经过点B.(1)求该抛物线的解析式;
(2)作直线BC∥x轴,交抛物线于点C,求线段BC的长.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:(1)先确定B(0,-2),A(-2,0),由于点A为顶点,则可是顶点式y=a(x+2)2,然后把B点坐标代入求出a即可;
(2)由于直线BC∥x轴,则C点坐标为-2,把y-2代入(1)中的解析式得到C点的纵坐标,然后计算BC的长.
(2)由于直线BC∥x轴,则C点坐标为-2,把y-2代入(1)中的解析式得到C点的纵坐标,然后计算BC的长.
解答:解:(1)令x=0,得y=-2,
∴B(0,-2),
令y=0,得x=-2,
∴A(-2,0),
设二次函数的解析式为y=a(x+2)2,
把B(0,-2)代入得4a=-2,解得a=-
,
∴抛物线的解析式为y=-
(x+2)2=-
x2-2x-2;
(2)令y=-2,得-
(x+2)2=-2,
解得x1=-4,x2=0,
∴BC=4.
∴B(0,-2),
令y=0,得x=-2,
∴A(-2,0),
设二次函数的解析式为y=a(x+2)2,
把B(0,-2)代入得4a=-2,解得a=-
| 1 |
| 2 |
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)令y=-2,得-
| 1 |
| 2 |
解得x1=-4,x2=0,
∴BC=4.
点评:本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(-2xy)2的计算结果是( )
| A、-2x2y2 |
| B、4x2y2 |
| C、4xy2 |
| D、-4xy2 |
计算:50×6-1=( )
A、
| ||
| B、0 | ||
| C、5 | ||
| D、不能确定 |
等腰直角三角形斜边为10,则它的直角边为( )
A、5
| ||
B、4
| ||
C、2
| ||
D、2
|
下列几种比较数的大小的方法:①倒数大的反而小;②绝对值大的反而小;③平方大的就大;④两数的商大于1时,被除数就大.其中正确的方法有( )
| A、0种 | B、1种 | C、2种 | D、3种 |
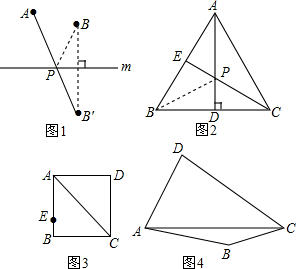 (1)观察发现:
(1)观察发现: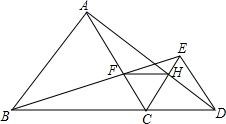 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,求证:FH∥BD.
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,求证:FH∥BD.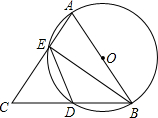 如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE. 下面是小马虎解的一道题
下面是小马虎解的一道题