题目内容
3.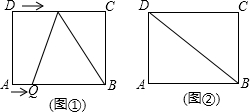 如图①,在长方形ABCD中,AB=8,AD=6.动点P、Q分别从点D、A同时出发向点C、B运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.设运动的时间为t(s)
如图①,在长方形ABCD中,AB=8,AD=6.动点P、Q分别从点D、A同时出发向点C、B运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.设运动的时间为t(s)(1)当t=2时,PQ的长为2$\sqrt{10}$;
(2)在运动过程中,若△BPQ为等腰三角形,求相应的时刻t;
(3)如图②,连接BD,是否存在某个时刻t,使得PQ垂直平分BD?若能,求t的值;若不能,说明理由.
分析 (1)作PH⊥AB于H,求出QH、PH,根据勾股定理求出PQ;
(2)分PQ=PB、BP=BQ和QP=QB三种情况进行分析即可;
(3)假设存在某个时刻t,使得PQ垂直平分BD,进行解答,看t是否存在即可.
解答 解:(1)如图①,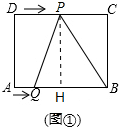 作PH⊥AB于H,
作PH⊥AB于H,
由题意得,DP=4,AQ=2,
则QH=2,又PH=AD=6,
由勾股定理的,PQ=$\sqrt{P{H}^{2}+Q{H}^{2}}$=2$\sqrt{10}$;
(2)当PQ=PB时,
如图①,QH=BH,
则t+2t=8,
解得,t=$\frac{8}{3}$;
当PQ=BQ时,
(2t-t)2+62=(8-t)2,
解得,t=$\frac{7}{4}$;
当BP=BQ时,
(8-2t)2+62=(8-t)2,
方程无解;
∴当t=$\frac{8}{3}$或$\frac{7}{4}$时,△BPQ为等腰三角形;
(3)假设PQ垂直平分BD,则QB=QD,PD=PB,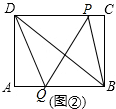
在Rt△ADQ中,t2+36=(8-t)2,
解得,t=$\frac{7}{4}$,
在Rt△CPB中,(8-2t)2+36=(2t)2,
解得,t=$\frac{25}{8}$,
∴不存在某个时刻t,使得PQ垂直平分BD.
点评 本题考查的是矩形的性质、等腰三角形的判定和垂直平分线的性质,掌握性质并灵活运用性质是解题的关键,注意分情况讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.计算a2•a4÷(-a2)2的结果是( )
| A. | a | B. | a2 | C. | -a2 | D. | a3 |
15.下列各式计算正确的是( )
| A. | (a2)3=a6 | B. | (π-1)0=0 | C. | a-1=-a(a≠0) | D. | (-2a)2=4a |
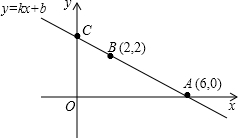 如图,一次函数y=kx+b的图象经过点A(6,0),点B(2,2),且与y轴相交于点C.请根据以上信息(不再添加其他条件),提出一个问题并尝试解答.你提出的问题是点C的坐标是什么;并请写出你的解答过程.
如图,一次函数y=kx+b的图象经过点A(6,0),点B(2,2),且与y轴相交于点C.请根据以上信息(不再添加其他条件),提出一个问题并尝试解答.你提出的问题是点C的坐标是什么;并请写出你的解答过程.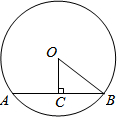 如图,AB是⊙O的弦,OC⊥AB,垂足为C.若AB=2,OC=$\sqrt{3}$,则∠COB的值为30°.?
如图,AB是⊙O的弦,OC⊥AB,垂足为C.若AB=2,OC=$\sqrt{3}$,则∠COB的值为30°.?