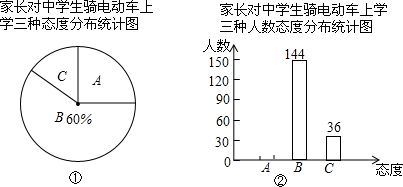
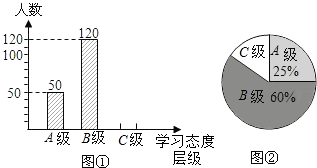
题目内容
8.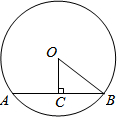 如图,AB是⊙O的弦,OC⊥AB,垂足为C.若AB=2,OC=$\sqrt{3}$,则∠COB的值为30°.?
如图,AB是⊙O的弦,OC⊥AB,垂足为C.若AB=2,OC=$\sqrt{3}$,则∠COB的值为30°.?
分析 由垂径定理得BC=$\frac{1}{2}$AB=1,由特殊角的三角函数知tan∠COB=$\frac{BC}{OC}$=$\frac{\sqrt{3}}{3}$,易得∠COB=30°.
解答 解:∵OC⊥AB,
∴BC=$\frac{1}{2}$AB=1,
∴tan∠COB=$\frac{BC}{OC}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠COB=30°.
故答案为:30°.
点评 本题主要考查了垂径定理和特殊角的三角函数,利用特殊角的三角函数是解答此题的关键.

练习册系列答案
相关题目
18.下列几何体中,主视图是矩形,俯视图是圆的几何体是( )
| A. | 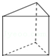 三棱柱 | B. |  圆柱 | C. |  长方体 | D. |  圆锥 |
18.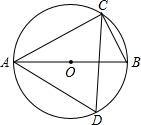 如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )
如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )
 如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )
如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )| A. | 52° | B. | 56° | C. | 62° | D. | 72° |
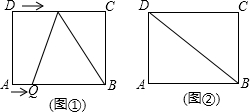 如图①,在长方形ABCD中,AB=8,AD=6.动点P、Q分别从点D、A同时出发向点C、B运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.设运动的时间为t(s)
如图①,在长方形ABCD中,AB=8,AD=6.动点P、Q分别从点D、A同时出发向点C、B运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.设运动的时间为t(s)