题目内容
12.在?ABCD中,AB=3,BC=4,当?ABCD的面积最大时,下列结论:①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
其中正确的有①②④.(填序号)
分析 由当?ABCD的面积最大时,AB⊥BC,可判定?ABCD是矩形,由矩形的性质,可得②④正确,③错误,又由勾股定理求得AC=5.
解答 解:∵当?ABCD的面积最大时,AB⊥BC,
∴?ABCD是矩形,
∴∠A=∠C=90°,AC=BD,故③错误,④正确;
∴∠A+∠C=180°;故②正确;
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,故①正确.
故答案为:①②④.
点评 此题考查了平行四边形的性质、矩形的判定与性质以及勾股定理.注意证得?ABCD是矩形是解此题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
2.某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误是( )
| A. | 众数是85 | B. | 平均数是85 | C. | 方差是20 | D. | 极差是15 |
1.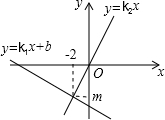 同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )
同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )
 同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )
同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )| A. | x>-2 | B. | x<-2 | C. | x<2 | D. | x<4 |
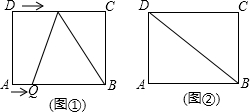 如图①,在长方形ABCD中,AB=8,AD=6.动点P、Q分别从点D、A同时出发向点C、B运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.设运动的时间为t(s)
如图①,在长方形ABCD中,AB=8,AD=6.动点P、Q分别从点D、A同时出发向点C、B运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.设运动的时间为t(s)