题目内容
17.(1)已知方程x2-2x+m-$\sqrt{2}$=0有两个相等的实数根,求m的值.(2)求代数式$\frac{m-1}{m}$÷(m-$\frac{2m-1}{m}$)的值,其中m为(1)中所得值.
分析 (1)由方程有两个相等的实数根可得知根的判别式△=0,代入数据即可得出关于m的一元一次方程,解方程即可得出结论;
(2)先将分式进行化解,再代入m的值,即可得出结论.
解答 解:(1)△=(-2)2-4×1×(m-$\sqrt{2}$)=4+4$\sqrt{2}$-4m,
∵方程有两个相等的实数根,
∴△=0,即4+4$\sqrt{2}$-4m=0,
解得:m=1+$\sqrt{2}$.
(2)∵$\frac{m-1}{m}$÷(m-$\frac{2m-1}{m}$),
=$\frac{m-1}{m}$÷$\frac{{m}^{2}-2m+1}{m}$,
=$\frac{m-1}{m}$×$\frac{m}{(m-1)^{2}}$,
=$\frac{1}{m-1}$.
∵m=1+$\sqrt{2}$,
∴$\frac{1}{m-1}$=$\frac{1}{1+\sqrt{2}-1}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了根的判别式以及分式的化简求值,解题的关键是:(1)得出关于m的一元一次方程;(2)将原分式化解.本题属于基础题,难度不大,解决该题型题目时,根据方程根的情况结合根的判别式得出方程(或不等式)是关键.

练习册系列答案
相关题目
12.不透明的袋子中装有10个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则( )
| A. | 这个球一定是黑球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球可能是白球 | |
| D. | 事先能确定摸到什么颜色的球 |
2.下列计算,正确的是( )
| A. | -|-3|=-3 | B. | 30=0 | C. | 3-1=-$\frac{1}{3}$ | D. | $\root{3}{9}$=3 |
9.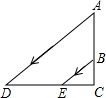 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )| A. | 1.5m | B. | 1.6m | C. | 1.86m | D. | 2.16m |
 如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里? 如图,四边形ABCD中,对角线AC,BD相交于点O,AD∥BC,OA=OC,AC平分∠BAD.欲使四边形ABCD是正方形,则还需添加添加AC=BD或∠BAD=90°(写出一个合适的条件即可)
如图,四边形ABCD中,对角线AC,BD相交于点O,AD∥BC,OA=OC,AC平分∠BAD.欲使四边形ABCD是正方形,则还需添加添加AC=BD或∠BAD=90°(写出一个合适的条件即可)