题目内容
17.如果反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-3,2),则它一定还经过( )| A. | (-$\frac{1}{2}$,8) | B. | (-3,-2) | C. | ($\frac{1}{2}$,12) | D. | (1,-6) |
分析 分别计算各点的横纵坐标之积,然后根据反比例函数图象上点的坐标特征进行判断.
解答 解:∵反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-3,2),
∴k=-3×2=-6,
∵-$\frac{1}{2}$×8=-4≠-6,
-3×(-2)=6≠-6,
$\frac{1}{2}×12$=6≠-6,
1×(-6)=-6,
则它一定还经过(1,-6),
故选D.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
9. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{AEB}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=60°,则∠ADC的度数是( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{AEB}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=60°,则∠ADC的度数是( )
 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{AEB}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=60°,则∠ADC的度数是( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是$\widehat{AEB}$上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=60°,则∠ADC的度数是( )| A. | 15 | B. | 20° | C. | 25° | D. | 30° |
7.-3是3的( )
| A. | 倒数 | B. | 绝对值 | C. | 相反数 | D. | 平方 |
 如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.
如图,?ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF.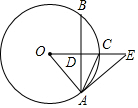 如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.
如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.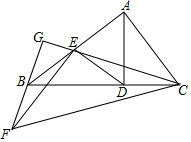 如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.
如图,Rt△ABC中,∠BAC=90°,过点A作AD⊥BC于点D,点E为线段AB中点,连接ED,EC将△EDC绕点E旋转,使点D和点B重合,得到△EBF,延长FB、CE相交于点G,若BC=$\sqrt{5}$,则BG=$\frac{\sqrt{5}}{3}$.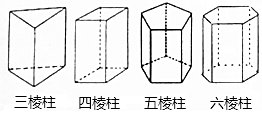 如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.