题目内容
12.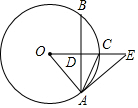 如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.
如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.(1)求证:直线AE是⊙O的切线,
(2)若AB=8,sin∠E=$\frac{2}{3}$,求⊙O的半径.
分析 (1)首先得出∠OCA+∠CAD=90°,进而求出∠EAC+∠OAC=90°,即可得出答案.
(2)作CF⊥AE于F,根据角平分线的性质和三角函数求得AE=$\frac{20}{3}$,DE=$\frac{16}{3}$,进一步求得CF=CD=2,然后根据勾股定理列出关于r的方程,解方程即可求得.
解答 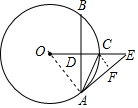 (1)证明:连接OA,
(1)证明:连接OA,
∵OE垂直于弦AB,
∴∠OCA+∠CAD=90°,
∵CO=OA,
∴∠OCA=∠OAC,
∵∠EAC=∠CAB,
∴∠EAC+∠OAC=90°,
∴OA⊥AE,
即直线AE是⊙O的切线.
(2)解:作CF⊥AE于F,
∵∠EAC=∠CAB,
∴CF=CD,
∵AB=8,
∴AD=4,
∵sin∠E=$\frac{3}{5}$,
∴$\frac{AD}{AE}$=$\frac{3}{5}$,$\frac{CF}{CE}$=$\frac{3}{5}$,
∴AE=$\frac{20}{3}$,DE=$\frac{16}{3}$,
∴CF=2,
∴CD=2,
设⊙O的半径r,
在RT△AOD中,OA2=OD2+AD2,即r2=(r-2)2+42,
解得r=5.
∴⊙O的半径为5.
点评 本题考查了切线的判定,角平分线的性质,三角函数的应用以及勾股定理的应用,熟练掌握这些性质定理是解题的关键.

练习册系列答案
相关题目
7.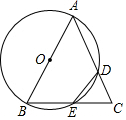 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
17.如果反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-3,2),则它一定还经过( )
| A. | (-$\frac{1}{2}$,8) | B. | (-3,-2) | C. | ($\frac{1}{2}$,12) | D. | (1,-6) |
 如图,AB∥CD,∠E=65°,则∠B+∠F+∠C=245°.
如图,AB∥CD,∠E=65°,则∠B+∠F+∠C=245°. 如图:
如图: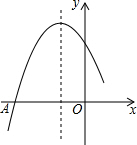 如图,二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.
如图,二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.