题目内容
17．x取哪些整数值时，不等式4（x+1）≤7x+10与x-5＜$\frac{x-8}{3}$都成立？分析 根据题意得出不等式组，解不等式组求得其解集即可．
解答 解：根据题意可得$\left\{\begin{array}{l}{4（x+1）≤7x+10}&{①}\\{x-5＜\frac{x-8}{3}}&{②}\end{array}\right.$，
解不等式①，得：x≥-2，
解不等式②，得：x＜3.5，
∴不等式组的解集为-2≤x＜3.5，
即当x取-2、-1、0、1、2、3时，不等式4（x+1）≤7x+10与x-5＜$\frac{x-8}{3}$都成立．
点评 本题主要考查解不等式组的能力，根据题意得出不等式组是解题的关键．
练习册系列答案
相关题目
解不等式$\frac{2x-1}{3}-\frac{9x+2}{6}≤1$，把它的解集在数轴上表示出来，并求出这个不等式的负整数解．
如图，在矩形纸片ABCD中，已知AD=8，折叠纸片，使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为（ ）
9．
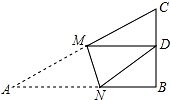如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）| A． | 4 | B． | 5 | C． | $\frac{5}{3}$ | D． | $\frac{5}{2}$ |
如图，将Rt△ABC绕直角顶点A顺时针旋转90°，得到△AB′C′，连结BB′，若∠1=20°，则∠C的度数是65°．
19．直角三角形的两直角边为a，b，斜边上的高为h，则下列各式中总是成立的是（ ）
| A． | $\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=\frac{1}{{h}^{2}}$ | B． | $\frac{1}{a}+\frac{1}{b}=\frac{1}{h}$ | C． | a2+b2=2ah | D． | $\frac{1}{a}+\frac{1}{b}=\frac{2}{h}$ |