题目内容
9.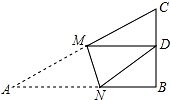 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )| A. | 4 | B. | 5 | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
分析 设BN=x,则由折叠的性质可得DN=AN=9-x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.
解答 解:设BN=x,由折叠的性质可得DN=AN=9-x,
∵D是BC的中点,
∴BD=3,
在Rt△NBD中,x2+32=(9-x)2,
解得x=4.
即BN=4.
故选A.
点评 此题考查了翻折变换(折叠问题),折叠的性质,勾股定理,中点的定义以及方程思想,综合性较强.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
18.二次根式$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>0 | B. | x≥2 | C. | x≥-2 | D. | x≤2 |
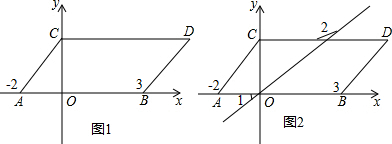 如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD. 如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象.
如图是一辆汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数图象. 如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为30.
如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为30.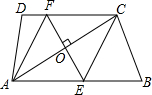 如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF.
如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF.