题目内容
19.直角三角形的两直角边为a,b,斜边上的高为h,则下列各式中总是成立的是( )| A. | $\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=\frac{1}{{h}^{2}}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{1}{h}$ | C. | a2+b2=2ah | D. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{h}$ |
分析 根据直角三角形的面积的计算方法,以及勾股定理就可解得.
解答 解:根据直角三角形的面积可以导出:c=$\frac{ab}{h}$.
再结合勾股定理:a2+b2=c2.
进行等量代换,得a2+b2=$\frac{{a}^{2}{b}^{2}}{{h}^{2}}$.
两边同除以a2b2,得$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.
故选A.
点评 本题主要考查了勾股定理,熟练运用勾股定理、直角三角形的面积公式以及等式的性质进行变形.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
18.二次根式$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>0 | B. | x≥2 | C. | x≥-2 | D. | x≤2 |
9.如图,将边长为 6 的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分为菱形时,则DA′为( )


| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$-1 | D. | 6$\sqrt{2}$-6 |
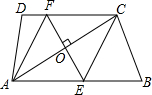 如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF.
如图,在四边形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB,CD于点E,F,连接CE,AF.