题目内容
观察下列各式及其验证过程:
=2
,验 证:
=
=
=2
;
=3
,验证:
=
=
=3
.
(1)根据以上两个等式及其验证过程的基本思路,猜想
的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为正整数)表示的等式,并给予证明.
1+
|
|
1+
|
|
|
|
2+
|
|
2+
|
|
|
|
(1)根据以上两个等式及其验证过程的基本思路,猜想
3+
|
(2)针对上述各式反映的规律,写出用n(n为正整数)表示的等式,并给予证明.
考点:二次根式的性质与化简
专题:规律型
分析:(1)根据已知计算过程求出即可;
(2)求出一般式子都是
=(n+1)
,根据已知算式的计算过程求出即可.
(2)求出一般式子都是
n+
|
|
解答:解:(1)
=4
,
理由是:
=
=
=4
;
(2)
=(n+1)
,
证明:
=
=
=(n+1)
3+
|
|
理由是:
3+
|
|
|
|
(2)
n+
|
|
证明:
n+
|
|
|
|
点评:本题考查了二次根式的性质的应用,主要考查学生的计算能力和阅读能力,难度适中.

练习册系列答案
相关题目
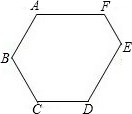 如图,在六边形ABCDEF中,AF∥CD,AB∥ED,∠A=140°,∠B=100°,∠E=90°.求∠C、∠D、∠F的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥ED,∠A=140°,∠B=100°,∠E=90°.求∠C、∠D、∠F的度数.