题目内容
10．
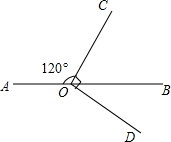如图，已知∠AOC=120°，∠COD是直角，∠BOC=2∠BOD．问点A、O、B在一条直线上吗？为什么？
分析 先根据∠COD是直角，∠BOC=2∠BOD可求得∠BOC=60°，然后可证明∠AOC+∠BOC=180°，从而可知点A、O、B在一条直线上．
解答 解：设∠BOD=x，则∠BOC=2x．
∵∠BOC+∠DOB=∠COD=90°，
∴2x+x=90°．
解得：x=30°．
∴∠BCO=2×30°=60°．
∴∠AOC+∠BOC=120°+60°=180°．
∴点A、O、B在一条直线上．
点评 本题主要考查的是角的计算，证得∠AOC+∠BOC=180°是解题的关键．
练习册系列答案
相关题目
1．大圩村某养殖葡萄户，从葡萄上市到销售完需20天，售价为15元/千克，销售情况在第x天的相关信息如下表所示：
（1）第几天每千克的利润最大；
（2）该养殖葡萄户，每天获得的利润为y（元），y关于x的关系是什么？第几天利润最大；
（3）该养殖葡萄户决定，每销售1千克捐养老院m（m≤2）元，满足每天获得的利润随x的增大而增大，求m的取值范围．
| 成本P（元/千克） | 8-$\frac{x}{10}$ |
| 采摘量q（千克） | 1000-10x |
（2）该养殖葡萄户，每天获得的利润为y（元），y关于x的关系是什么？第几天利润最大；
（3）该养殖葡萄户决定，每销售1千克捐养老院m（m≤2）元，满足每天获得的利润随x的增大而增大，求m的取值范围．
15．化简：$\sqrt{（1-sin52°）^{2}}$-$\sqrt{（1-tan52°）^{2}}$的结果是（ ）
| A． | tan52°-sin52° | B． | sin52°-tan52° | C． | 2-sin52°-tan52° | D． | -sin52°-tan52° |
19．已知$\left\{\begin{array}{l}{x+2y=-4m}\\{2x+y=2m+1}\end{array}\right.$，且x-y＜0，则m的取值范围为（ ）
| A． | m$＜\frac{1}{2}$ | B． | m$＞\frac{1}{2}$ | C． | m$＞-\frac{1}{2}$ | D． | m$＜-\frac{1}{6}$ |