题目内容
6.某商店购进一批单价为8元的商品,如果每件按10元出售每天可销售100件.市场调查反映:如调整价格,每涨价1元,每天要少卖出10件,设每件售价为x元.(1)请用含x的式子表示:①销售该商品每件的利润是(x-8)元;②每天的销量是(200-10x)件;(直接写出结果)
(2)设销售该商品的日利润为y元,那么售价为多少元时,当天的销售利润最大,最大利润是多少?
分析 (1)每件的利润=售价-进价,根据每涨价1元,每天要少卖出10件可求得销售的数量;
(2)根据商品的利润=每件的利润×售出商品的数量列出函数关系式,然后利用配方法可求得最大值.
解答 解:(1)商品每件的利润=x-8;每天的销量=100-10(x-10)=200-10x.
故答案为:(x-8);200-10x.
(2)y=(200-10x)•(x-8)
=-10x2+280x-1600
=-10(x-14)2+360.
所以将销售定价定为14元时,每天所获销售利润最大,且最大利润是360元.
点评 本题主要考查的是二次函数的应用,列出利润y与售价x的函数关系式是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
16.一个多边形从一个顶点出发共引7条对角线,那么这个多边形是为( )
| A. | 7边形 | B. | 8边形 | C. | 9边形 | D. | 10边形 |
14.为认真贯彻落实党的十八大和中央政治局关于八项规定的精神,厉行节约、反对铺张浪费,某市严格控制“三公”经费支出,共节约“三公”经费5.05亿元.用科学记数法表示为( )
| A. | 505×106元 | B. | 5.05×107元 | C. | 50.5×107元 | D. | 5.05×108元 |
1.大圩村某养殖葡萄户,从葡萄上市到销售完需20天,售价为15元/千克,销售情况在第x天的相关信息如下表所示:
(1)第几天每千克的利润最大;
(2)该养殖葡萄户,每天获得的利润为y(元),y关于x的关系是什么?第几天利润最大;
(3)该养殖葡萄户决定,每销售1千克捐养老院m(m≤2)元,满足每天获得的利润随x的增大而增大,求m的取值范围.
| 成本P(元/千克) | 8-$\frac{x}{10}$ |
| 采摘量q(千克) | 1000-10x |
(2)该养殖葡萄户,每天获得的利润为y(元),y关于x的关系是什么?第几天利润最大;
(3)该养殖葡萄户决定,每销售1千克捐养老院m(m≤2)元,满足每天获得的利润随x的增大而增大,求m的取值范围.
15.化简:$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$的结果是( )
| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
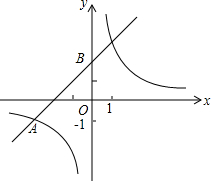 如图,在平面直角坐标系xoy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+2的图象的一个交点为A(m,-1).
如图,在平面直角坐标系xoy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+2的图象的一个交点为A(m,-1).