题目内容
18．
如图，数轴上点A对应的数为2，AB⊥OA于A，且AB=1，以点O为圆心，以OB为半径画弧，交正半轴于点C，则点C对应的数为（ ）| A． | 3 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
分析 根据题意运用勾股定理求出OB的长，得到答案．
解答 解：在Rt△OAB中，OA=2，AB=1，
由勾股定理得，OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{5}$，
故选：D．
点评 本题考查的是实数与数轴的关系，正确运用勾股定理求出OB的长是解题的关键，要理解数轴上的点与实数的对应关系．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
8．
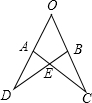如图，OA=OB，OC=OD，∠O=50°，∠D=35°，则∠OAC等于（ ）
如图，OA=OB，OC=OD，∠O=50°，∠D=35°，则∠OAC等于（ ）| A． | 65° | B． | 95° | C． | 45° | D． | 100° |
如图所示，△A′B′C′是△ABC经过平移得到的，A（-4，-1），B（-5，-4），C（-1，-3），△ABC中任意一点P（x1，y1）平移后的对应点为P′（x1+6，y1+4）．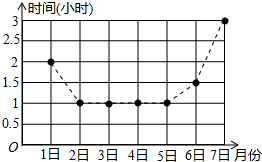
如图是小浩同学8月1日〜7日毎天的自主学习时间统计图，则小浩同学一天中自主学习时间最长是3小时，这七天平均每天的自主学习时间是1.5小时．
10．在平面直角坐标系中，点P（-2，3）到x轴的距离为（ ）
| A． | -2 | B． | 2 | C． | -3 | D． | 3 |
如图，A、C在?BFDE的对角线EF所在的直线上，且AE=CF，求证：BC∥AD．