题目内容
13.已知$\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$=2,则$\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$的值为5.分析 根据题意,$\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$=2,变形为$\sqrt{25-{x}^{2}}$=$\sqrt{15-{x}^{2}}$+2,两边平方得x2=$\frac{51}{4}$,代入求值即可.
解答 解:∵$\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$=2,
∴$\sqrt{25-{x}^{2}}$=$\sqrt{15-{x}^{2}}$+2,
两边平方得,25-x2=4+15-x2+4$\sqrt{15-{x}^{2}}$,
∴2$\sqrt{15-{x}^{2}}$=3,
两边平方得4(15-x2)=9,
化简,得x2=$\frac{51}{4}$,
∴$\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$=$\frac{7}{2}$+$\frac{3}{2}$=5.
故答案为:5.
点评 本题考查了二次根式的化简求值,根据二次根式的乘除法法则进行二次根式有理化.所以一般二次根式的有理化因式是符合平方差公式的特点的式子.

练习册系列答案
相关题目
4.下列多项式中不能用公式分解的是( )
| A. | a2+a+$\frac{1}{4}$ | B. | -a2+b2-2ab | C. | -a2+25b2 | D. | -4+b2 |
8.在平面直角坐标系中,将点P(-4,1)向右平移3个单位长度,再向上平移4个单位长度得到点P的坐标是( )
| A. | (0,4) | B. | (-1,5 ) | C. | (-1,-3) | D. | (-3,5) |
18. 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以点O为圆心,以OB为半径画弧,交正半轴于点C,则点C对应的数为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以点O为圆心,以OB为半径画弧,交正半轴于点C,则点C对应的数为( )
 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以点O为圆心,以OB为半径画弧,交正半轴于点C,则点C对应的数为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以点O为圆心,以OB为半径画弧,交正半轴于点C,则点C对应的数为( )| A. | 3 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
2.我县举行了一次艺术比赛,各年级组的参赛人数如下表所示:
(1)求全体参赛选手年龄的众数,中位数.
(2)王涛说,他所在年龄组的参赛人数占全体参赛人数的24%,你认为王涛是哪个年龄组的选手?请说明理由.
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 5 | 19 | 12 | 14 |
(2)王涛说,他所在年龄组的参赛人数占全体参赛人数的24%,你认为王涛是哪个年龄组的选手?请说明理由.
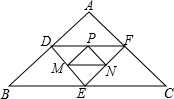 如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( )
如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( ) 如图所示的是某年参加国际教育评估的15个国家学生的数学平均成绩的统计图,则平均成绩大于或等于60的国家个数是12.
如图所示的是某年参加国际教育评估的15个国家学生的数学平均成绩的统计图,则平均成绩大于或等于60的国家个数是12.