题目内容
2.某商店试销一种成本为10元的文具.经试销发现,每天销售件数y(件)是每件销售价格x(元)的一次函数,且当每件按15元的价格销售时,每天能卖出50件;当每件按20元的价格销售时,每天能卖出40件.(1)试求y关于x的函数解析式(不用写出定义域);
(2)如果每天要通过销售该种文具获得450元的利润,那么该种文具每件的销售价格应该定为多少元?(不考虑其他因素)
分析 (1)设出一次函数解析式y=kx+b,用待定系数法建立关于k和b的方程组,解之即可求出所求;
(2)按照等量关系“每月获得的利润=(销售价格-进价)×销售件数”列出二次函数,并求得最值.
解答 解:(1)由题意,知:当x=15时,y=50;当x=20时,y=40,
设所求一次函数解析式为y=kx+b,
由题意得:$\left\{\begin{array}{l}{15k+b=50}\\{20k+b=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=80}\end{array}\right.$
∴所求的y关于x的函数解析式为y=-2x+80.
(2)由题意,可得:(x-10)(-2x+80)=450
解得:x=25
答:该种文具每件的销售价格应该定为25元.
点评 本题考查了二次函数在实际生活中的应用,重点是掌握求最值的问题.注意:数学应用题来源于实践,用于实践,在当今社会市场经济的环境下,应掌握一些有关商品价格和利润的知识,总利润等于总收入减去总成本,然后再利用二次函数求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.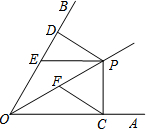 如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )
 如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )| A. | 6 | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
 如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.
如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.