题目内容
6. 如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D与点B重合,则重叠部分(△BEF)的面积为7.5cm2.
如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D与点B重合,则重叠部分(△BEF)的面积为7.5cm2.
分析 设DE=xcm,由翻折的性质可知DE=EB=x,则AE=(9-x)cm,在Rt△ABE中,由勾股定理求得ED的长;由翻折的性质可知∠DEF=∠BEF,由矩形的性质可知BC∥AD,从而得到∠BFE=∠DEF,故此可知∠BFE=∠FEB,得出FB=BE,最后根据三角形的面积公式求解即可.
解答 解:设DE=xcm.
由翻折的性质可知DE=EB=x,∠DEF=∠BEF,则AE=(9-x)cm.
在Rt△ABE中,由勾股定理得;BE2=EA2+AB2,即x2=(9-x)2+32.
解得:x=5.
∴DE=5cm.
∵四边形ABCD为矩形,
∴BC∥AD.
∴∠BFE=∠DEF.
∴∠BFE=∠FEB.
∴FB=BE=5cm.
∴△BEF的面积=$\frac{1}{2}$BF•AB=$\frac{1}{2}$×3×5=7.5(cm2);
故答案为:7.5.
点评 本题主要考查的是翻折的性质、勾股定理的应用,等腰三角形的判定、三角形的面积公式,证得△BEF为等腰三角形,从而得到FB的长是解题的关键.

练习册系列答案
相关题目
17.某体育用品商店为了解5月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下两幅不完整的统计图

(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按5月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种球,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如表:
求出y与x之间的函数关系式;
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.

(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按5月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种球,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如表:
| 类别 | 篮球 | 足球 | 排球 |
| 进价(单位:元/个) | 50 | 30 | 20 |
| 预售价(单位:元/个) | 70 | 45 | 25 |
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.
18.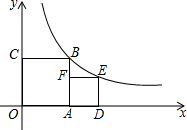 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )| A. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ | B. | $({\frac{{\sqrt{5}+1}}{2},\frac{{\sqrt{5}-1}}{2}})$ | C. | $({\frac{{\sqrt{5}}}{2},-\frac{{\sqrt{5}}}{2}})$ | D. | (1,1) |
 如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证: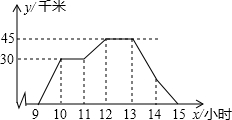 A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )
A、B两地路程为45千米,图中折线表示骑车人离A地的路程y与时间x的函数关系,一辆客车10:30从A地出发,沿与骑车人相同的路线以45千米/时的速度往返于A、B两地之间(往返中不停留),以下结论正确的个数有( )