题目内容
 如图,在四边形ABCD中,AB+CD<AD,AE平分∠BAD,DE平分∠CDA,E是BC中点,∠AED=120°,求证:AB+CD+
如图,在四边形ABCD中,AB+CD<AD,AE平分∠BAD,DE平分∠CDA,E是BC中点,∠AED=120°,求证:AB+CD+| 1 |
| 2 |
考点:全等三角形的判定与性质
专题:证明题
分析:在AD上分别截取AM=AB,DN=DC,(M、N均在AD上),连接EM,EN;先证明△ABE≌△AME和△NDE≌△CDE,证出EM=EN,再证∠MEN=60°,证出△MEN为等边三角形,得出MN=EM=EN,即可证出结论.
解答:
证明:在AD上分别截取AM=AB,DN=DC,(M、N均在AD上),连接EM,EN;如图所示:
 ∵AE平分∠BAD,DE平分∠CDA,
∵AE平分∠BAD,DE平分∠CDA,
∴∠BAE=∠MAE,∠NDE=∠CDE,
在△ABE和△AME中,
,
∴△ABE≌△AME(SAS),
∴BE=ME,∠AEB=∠AEM,
在△NDE和△CDE中,
,
∴△NDE≌△CDE,
∴EN=EC,∠DEN=∠DEC,
∵E是BC中点,
∴BE=EC,
∴EM=EN,
∵∠MEN+∠AEM+∠DEN=120°①,
∠MEN+2∠AEM+2∠DEN=180°②,
∴①×2-②得:∠MEN=60°,
∴△MEN为等边三角形,
∴MN=EM=EN,
∴MN=BE,
∴AB+CD+
BC=AM+DN+MN=AD.
 ∵AE平分∠BAD,DE平分∠CDA,
∵AE平分∠BAD,DE平分∠CDA,∴∠BAE=∠MAE,∠NDE=∠CDE,
在△ABE和△AME中,
|
∴△ABE≌△AME(SAS),
∴BE=ME,∠AEB=∠AEM,
在△NDE和△CDE中,
|
∴△NDE≌△CDE,
∴EN=EC,∠DEN=∠DEC,
∵E是BC中点,
∴BE=EC,
∴EM=EN,
∵∠MEN+∠AEM+∠DEN=120°①,
∠MEN+2∠AEM+2∠DEN=180°②,
∴①×2-②得:∠MEN=60°,
∴△MEN为等边三角形,
∴MN=EM=EN,
∴MN=BE,
∴AB+CD+
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质以及等边三角形的判定与性质;通过作辅助线证明三角形全等和等边三角形是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列说法错误的是( )
| A、若a=b,则a+1=b+1 | ||||
| B、若a=b,则a(x2+1)=b(x2+1) | ||||
C、若a=b,则
| ||||
| D、若a(x-1)=b(x-1),则a=b |
 BE、CF分别是△ABC的中线,且BE=CF,AM⊥CF于M,AN⊥BE于N,求证:AM=AN.
BE、CF分别是△ABC的中线,且BE=CF,AM⊥CF于M,AN⊥BE于N,求证:AM=AN. E是正方形对角线DB延长线上的一点,以AE为边作等边三角形△AEF,连接CE,CF.CF与AE交于点O.求证:EF=CE.
E是正方形对角线DB延长线上的一点,以AE为边作等边三角形△AEF,连接CE,CF.CF与AE交于点O.求证:EF=CE.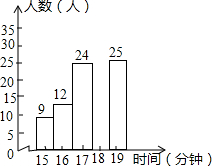 为解决“一票难求”的烦恼,2012年1月1日起,火车票实名制在全国范围内开始实施,某火车站为了改进服务,随机抽查了100名旅客从开始在购票窗口排队到购车票所用的时间t(简称为购票时间,单位:分钟),如图是这次调查数据整理后得到的统计图,请你根据图中的信息,回答下列问题:
为解决“一票难求”的烦恼,2012年1月1日起,火车票实名制在全国范围内开始实施,某火车站为了改进服务,随机抽查了100名旅客从开始在购票窗口排队到购车票所用的时间t(简称为购票时间,单位:分钟),如图是这次调查数据整理后得到的统计图,请你根据图中的信息,回答下列问题: