题目内容
如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
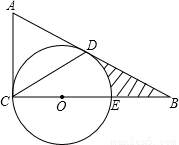
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
(1)证明见解析;(2)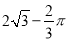 .
.
【解析】
试题分析:(1)连接OD,求出∠ODB=90°,求出∠B=30°,∠DOB=60°,求出∠DCB度数,关键三角形内角和定理求出∠A,即可得出答案;
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案.
试题解析:(1)证明:连接OD,
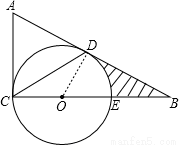
∵AB是⊙O切线,
∴∠ODB=90°,
∴BE=OE=OD=2,
∴∠B=30°,∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC=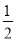 ∠DOB=30°,
∠DOB=30°,
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∴∠A=2∠DCB;
(2)【解析】
∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2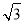 ,
,
∴阴影部分的面积S=S△ODB-S扇形DOE=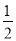 ×2
×2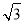 ×2-
×2-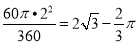 .
.
考点:1.切线的性质;2.扇形面积的计算.

练习册系列答案
相关题目
 ”的运算法则为:
”的运算法则为: ,则
,则 。
。
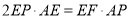 ?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
 如图,在四边形ABCD中,AB+CD<AD,AE平分∠BAD,DE平分∠CDA,E是BC中点,∠AED=120°,求证:AB+CD+
如图,在四边形ABCD中,AB+CD<AD,AE平分∠BAD,DE平分∠CDA,E是BC中点,∠AED=120°,求证:AB+CD+