题目内容
16.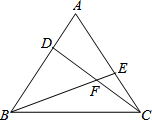 如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.
如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.(1)求证:△ACD≌△CBE;
(2)蜗牛在爬行过程中,DC与BE所成的∠BFC的大小有无变化?请证明你的结论.
分析 (1)根据SAS即可判断出△ACD≌△CBE;
(2)根据△ACD≌△CBE,可知∠BFC=180°-∠FBC-∠BCD=180°-∠ACD-∠BCD.
解答 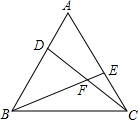 (1)证明:∵AB=BC=CA,两只蜗牛速度相同,且同时出发,
(1)证明:∵AB=BC=CA,两只蜗牛速度相同,且同时出发,
∴CE=AD;∠A=∠BCE=60°,
在△ACD与△CBE中,
$\left\{\begin{array}{l}{AC=CB}\\{∠A=∠BCE}\\{CE=AD}\end{array}\right.$,
∴△ACD≌△CBE(SAS);
(2)解:DC和BE所成的∠BFC的大小不变.
理由如下:∵△ACD≌△CBE,
∴∠BFC=180°-∠FBC-∠BCD=180°-∠ACD-∠BCD=120°.
点评 本题考查全等三角形的应用及等边三角形的性质,难度适中,求解第二问时找出∠BFC=180°-∠FBC-∠BCD=180°-∠ACD-∠BCD是关键.

练习册系列答案
相关题目
1. 在平面直角坐标系xOy中,已知点B(0,2),点A在x轴正半轴上且∠BAO=30°.将△OAB沿直线AB折叠得△CAB,则点C的坐标为( )
在平面直角坐标系xOy中,已知点B(0,2),点A在x轴正半轴上且∠BAO=30°.将△OAB沿直线AB折叠得△CAB,则点C的坐标为( )
 在平面直角坐标系xOy中,已知点B(0,2),点A在x轴正半轴上且∠BAO=30°.将△OAB沿直线AB折叠得△CAB,则点C的坐标为( )
在平面直角坐标系xOy中,已知点B(0,2),点A在x轴正半轴上且∠BAO=30°.将△OAB沿直线AB折叠得△CAB,则点C的坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,3) | C. | (3,$\sqrt{3}$) | D. | ($\sqrt{3}$,1) |
6.“掷实心球”是我市初中毕业生体育测试项目之一.测试时,记录下学生掷实心球的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生掷实心球的评分标准如下:
某校九年级有500名男生参加掷实心球模拟测试,现从中随机抽取10名男生测试成绩(单位:米)如下:
7.39 8.69 9.41 7.50 8.50 7.89 11.11 8.31 6.09 8.11
请完成下列问题:
(1)求这10名男生掷实心球成绩的平均数;
(2)这10名男生掷实心球得分的众数是10,中位数是9;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这500名男生在这次模拟测试中得优秀的人数.
| 成绩(米) | … | 6.00~6.49 | 6.50~6.99 | 7.00~7.49 | 7.50~7.99 | 8.00~8.49 | 8.50及以上 |
| 得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
7.39 8.69 9.41 7.50 8.50 7.89 11.11 8.31 6.09 8.11
请完成下列问题:
(1)求这10名男生掷实心球成绩的平均数;
(2)这10名男生掷实心球得分的众数是10,中位数是9;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这500名男生在这次模拟测试中得优秀的人数.
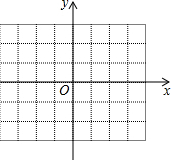 如图是一个平面直角坐标系,在坐标系中描出下列各点:A(1,2),B(3,2),C(-1,1),D(-1,-2).
如图是一个平面直角坐标系,在坐标系中描出下列各点:A(1,2),B(3,2),C(-1,1),D(-1,-2).