题目内容
15.已知关于x、y的方程组$\left\{\begin{array}{l}{2x+4y=20}\\{ax+by=1}\end{array}\right.$与$\left\{\begin{array}{l}{2x-y=5}\\{bx+ay=6}\end{array}\right.$有相同的解,则a+b=1.分析 联立方程组中两个不含a与b的方程组成方程组,求出方程组的解得到x与y的值,代入剩下方程求出a与b的值,即可求出a+b的值.
解答 解:联立得:$\left\{\begin{array}{l}{x+2y=10①}\\{2x-y=5②}\end{array}\right.$,
①+②×2得:5x=20,
解得:x=4,
把x=4代入①得:y=3,
把x=4,y=3代入得:$\left\{\begin{array}{l}{4a+3b=1}\\{3a+4b=6}\end{array}\right.$,
两方程相加得:7(a+b)=7,
解得:a+b=1,
故答案为:1
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
4.若2x+3y-z-2=0,则16x×82y÷4z的值是( )
| A. | 16 | B. | -16 | C. | 8 | D. | -8 |
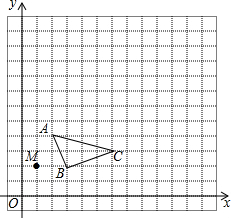 已知:△ABC和点M(1,2),
已知:△ABC和点M(1,2),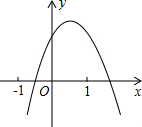 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②c>0;③a-b+c<0;④b2-4ac>0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②c>0;③a-b+c<0;④b2-4ac>0,其中正确的个数是( )