题目内容

5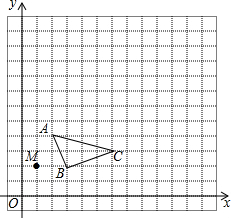．已知：△ABC和点M（1，2），
（1）以点M为位似中心，画出△ABC的一个位似图形△A′B′C′，使△A′B′C′与△ABC相似比为2：1；
（2）直接写出点C′的坐标．

分析 （1）延长MA到A′使MA′=2MA，则点A′为点A的对应点，同样方法得到点B、C的对应点B′、C′，从而得到△A'B'C'；
（2）利用第一象限点的坐标特征，写出△A'B'C'的顶点C'的坐标．

解答 解：（1）如图，△A′B′C′为所作；

（2）由图可得，C′（11，4）．

点评 本题考查了作图-位似变换，先确定位似中心；再分别连接并延长位似中心和能代表原图的关键点；接着根据位似比，确定能代表所作的位似图形的关键点；然后顺次连接上述各点，得到放大或缩小的图形．

练习册系列答案
相关题目
8．如图所示，将△OBA进行怎样的平移可得到△O′B′A′？并分别写出△OBA和△O′B′A′各顶点的坐标．
16．已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上的一动点（点D不与点B，C重合）．以AD为边作正方形ADEF，连结CF．
（1）如图1，当点D在线段BC上时，求证：CF+CD=BC；
（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的等量关系；
（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；
①请直接写出CF，BC，CD三条线段之间的关系；
②若正方形ADEF的边长为2，对角线AE，DF相较于点O，连结OC，求OC的长度．
13．计算：
（1）（-$\frac{1}{36}$）÷（$\frac{2}{9}$-$\frac{1}{4}$+$\frac{1}{18}$）               
 （2）-14+（1-0.5）×$\frac{1}{3}$×[2-（-3）2]
（3）解方程：$\frac{2x+1}{3}$-$\frac{5x-1}{6}$=1           
（4）$\frac{2（x+3）}{5}$=$\frac{3}{2}$x-$\frac{2（x-7）}{3}$．
20．如图1，在△ABC中，AB=AC，点D，F是射线AB上的动点，点E是射线AC上的动点，且DA=DE，EA=EF，设AE=4t．△DEF与△ABC重叠面积为y，如图2是y关于t的函数图象（其中0≤t≤$\frac{5}{4}$，$\frac{5}{4}$＜t≤2，2＜t≤m时，函数的解析式不同）．
（1）m=$\frac{16}{5}$，n=$\frac{117}{16}$；
（2）求y关于t的函数关系式．
10．在平面直角坐标系中，若点A（a，-b）在第一象限内，则点B（b，-a）在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
17．若抛物线y=ax2+bx+c与y轴的交点的坐标为（0，-3），则c=-3．
14．已知，在平面直角坐标系中，点P（x，y）的坐标x，y满足y=$\sqrt{x-2}$+$\sqrt{2-x}$-4；求点P到原点的距离．
15．已知关于x、y的方程组$\left\{\begin{array}{l}{2x+4y=20}\\{ax+by=1}\end{array}\right.$与$\left\{\begin{array}{l}{2x-y=5}\\{bx+ay=6}\end{array}\right.$有相同的解，则a+b=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网