题目内容
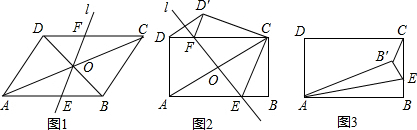
16.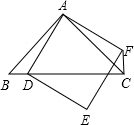 如图所示,四边形ADEF为正方形,△ABC为等腰直角三角形,D在BC边上,连接CF.
如图所示,四边形ADEF为正方形,△ABC为等腰直角三角形,D在BC边上,连接CF.(1)求证:BC⊥CF;
(2)若△ABC的面积为16,BD:DC=1:3,求正方形ADEF的面积;
(3)当(2)的条件下,连接AE交DC于G,求$\frac{DG}{GC}$的值.
分析 (1)由正方形的性质及等腰直角三角形的性质证明△ABD≌△ACF即可;
(2)由三角形的面积可以求出AB、AC的值,由勾股定理就可以求出BC的值,就可以求出BD、CD的值,作DH⊥AB于点H,由勾股定理就可以求出BH=DH的值,进而得出AH的值,由勾股定理就可以求出AD2的值,即可得出结论;
(3)设EF交BC于点M,设CM=x,则可以表示出MD,由勾股定理就可以得出FM的值,由△FCM∽△DEF就可以得出x的值,再由△AGD∽△EGM就可以得出GM的值,进而求出结论.
解答 解:(1)∵四边形ADEF为正方形,△ABC为等腰直角三角形,
∴AD=AF=EF=DE,AB=AC,∠DAF=∠BAC=∠DEF=∠ADE=90°,∠B=∠ACB=45°,AD∥EF.
∴∠DAF-∠DAC=∠BAC-∠DAC,
∴∠DAB=∠FAC.
在△ABD和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠DAB=∠FAC}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACF(SAS),
∴∠B=∠ACF,BD=CF,
∴∠ACF=45°,
∴∠ACF+∠ACB=90°,
即∠BCF=90°.
∴BC⊥CF;
(2)设AB=BC=x,由题意,得
$\frac{{x}^{2}}{2}$=16,
∴x=4$\sqrt{2}$.
∴BC=8.
∵BD:DC=1:3,
∴BD=8×$\frac{1}{4}$=2,CD=8-2=6.
作DH⊥AB于点H,
∴∠DHB=∠DHA=90°,
∴∠BDH=45°,
∴∠B=∠BDH,
∴BH=DH.
设BH=DH=a,由勾股定理,得
a=$\sqrt{2}$,
∴AH=4$\sqrt{2}$-$\sqrt{2}$=3$\sqrt{2}$.
在Rt△ADH中,由勾股定理,得
AD2=20.
∴AD=2$\sqrt{5}$.
∵S正方形ADEF=AD2,
∴正方形ADEF的面积为20;
(3)设EF交BC于点M,设CM=x,则DM=6-x.
∵BD=CF,
∴CF=2.
在Rt△CMF中,由勾股定理,得
FM=$\sqrt{4+{x}^{2}}$.
∵∠DEF=∠FCM=90°,
∠DME=∠FMC,
∴△FCM∽△DEM,
∴$\frac{FM}{DM}=\frac{FC}{DE}$,
∴$\frac{F{M}^{2}}{D{M}^{2}}=\frac{F{C}^{2}}{D{E}^{2}}$,
∴$\frac{4+{x}^{2}}{(6-x)^{2}}=\frac{4}{20}$,
解得:x1=1,x2=-4(舍去)
∴CM=1,FM=$\sqrt{5}$,
∴ME=$\sqrt{5}$.DM=5
∵AD∥EF.
∴△AGD∽△EGM,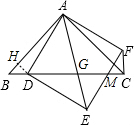
∴$\frac{DG}{GM}=\frac{AD}{EM}$,
∴$\frac{DG}{GM}=\frac{2\sqrt{5}}{\sqrt{5}}$=2,
∴DG=2GM,
设GM=b,DG=2b,
∴b+2b=5,
∴b=$\frac{5}{3}$,
∴GC=$\frac{5}{3}+1=\frac{8}{3}$,
∴DG=6-$\frac{8}{3}$=$\frac{10}{3}$.
∴$\frac{DG}{GC}=\frac{\frac{10}{3}}{\frac{8}{3}}$=$\frac{5}{4}$.
答:$\frac{DG}{GC}$的值为$\frac{5}{4}$.
点评 本题考查了正方形的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,垂直的判定及性质的运用,相似三角形的判定及性质的运用,三角形的面积公式的运用,解答时证明三角形全等及相似是关键.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案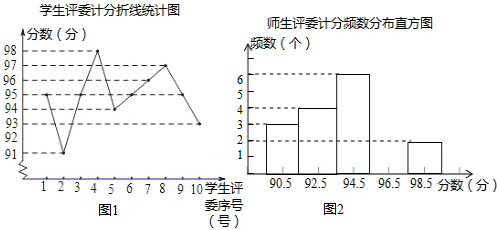
老师评委计分统计表
| 评委序号(号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 计分(分) | 94 | 96 | 93 | 91 | x | 91 | 91 | 98 | 96 | 93 |
(2)学生评委计分的中位数是95分
(3)计算各班最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,然后计算平均数:分别计算老师、学生评委的平均分:老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知七(1)班租后得分为94.4分,求统计表中x的值.
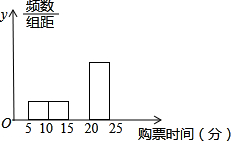 某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到够到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:
某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到够到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:(1)在表中填写确实的数据并补全频率分布直方图;
(2)旅客购票所用的时间平均数可能落在第4组;
(3)若每增加一个购票窗口可以使平均购票用时降低5分钟,要使平均购票用时不超过10分钟,那么请你估计最少需增加几个窗口?
| 分 组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | 0.10 |
| 四组 | 15≤t<20 | 50 | 0.50 |
| 五组 | 20≤t<25 | 30 | 0.30 |
| 合 计 | 100 | 1 |
| A. | (-2,3) | B. | (1,5) | C. | (1,6) | D. | (1,-6) |
| A. | y1>y2>0 | B. | y1<y2<0 | C. | y2>y1>0 | D. | y2<y1<0 |
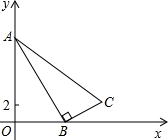 如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).
如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).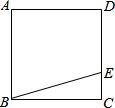 如图,E为正方形ABCD的边CD上一点,将△BCE绕C点顺时针旋转90°后得到△DCF,则此时BE与DF的关系为相等、垂直.
如图,E为正方形ABCD的边CD上一点,将△BCE绕C点顺时针旋转90°后得到△DCF,则此时BE与DF的关系为相等、垂直.